LC 1670. 设计前中后队列

题目描述

这是 LeetCode 上的 1670. 设计前中后队列 ，难度为 中等。

请你设计一个队列，支持在前，中，后三个位置的 push 和 pop 操作。

请你完成 FrontMiddleBack 类：

  • FrontMiddleBack() 初始化队列。
  • void pushFront(int val) 将 val 添加到队列的 最前面 。
  • void pushMiddle(int val) 将 val 添加到队列的 正中间 。
  • void pushBack(int val) 将 val 添加到队里的 最后面 。
  • int popFront() 将最前面的元素从队列中删除并返回值，如果删除之前队列为空，那么返回 -1。
  • int popMiddle() 将正中间的元素从队列中删除并返回值，如果删除之前队列为空，那么返回 -1。
  • int popBack() 将 最后面 的元素从队列中删除并返回值，如果删除之前队列为空，那么返回 -1。

请注意当有 两个 中间位置的时候，选择靠前面的位置进行操作。比方说：

  • 将 6 添加到 [1, 2, 3, 4, 5] 的中间位置，结果数组为 [1, 2, 6, 3, 4, 5]。
  • 从 [1, 2, 3, 4, 5, 6] 的中间位置弹出元素，返回 3，数组变为 [1, 2, 4, 5, 6]。

示例 1：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
输入：
["FrontMiddleBackQueue", "pushFront", "pushBack", "pushMiddle", "pushMiddle", "popFront", "popMiddle", "popMiddle", "popBack", "popFront"]
[[], [1], [2], [3], [4], [], [], [], [], []]

输出：
[null, null, null, null, null, 1, 3, 4, 2, -1]

解释：
FrontMiddleBackQueue q = new FrontMiddleBackQueue();
q.pushFront(1);   // [1]
q.pushBack(2);    // [1, 2]
q.pushMiddle(3);  // [1, 3, 2]
q.pushMiddle(4);  // [1, 4, 3, 2]
q.popFront();     // 返回 1 -> [4, 3, 2]
q.popMiddle();    // 返回 3 -> [4, 2]
q.popMiddle();    // 返回 4 -> [2]
q.popBack();      // 返回 2 -> []
q.popFront();     // 返回 -1 -> [] （队列为空）

提示：

  • $1 <= val <= 10^9$
  • 最多调用 $1000$ 次 pushFront， pushMiddle， pushBack， popFront， popMiddle 和 popBack。

双端队列

只要求在头部或尾部高效插入/弹出元素的话，容易联想到双端队列。

还需要考虑往中间插入/弹出元素的话，会想到使用两个双端队列。

将两个双端队列分别称为 l 和 r，把 l 和 r 拼接起来就是完整元素列表：

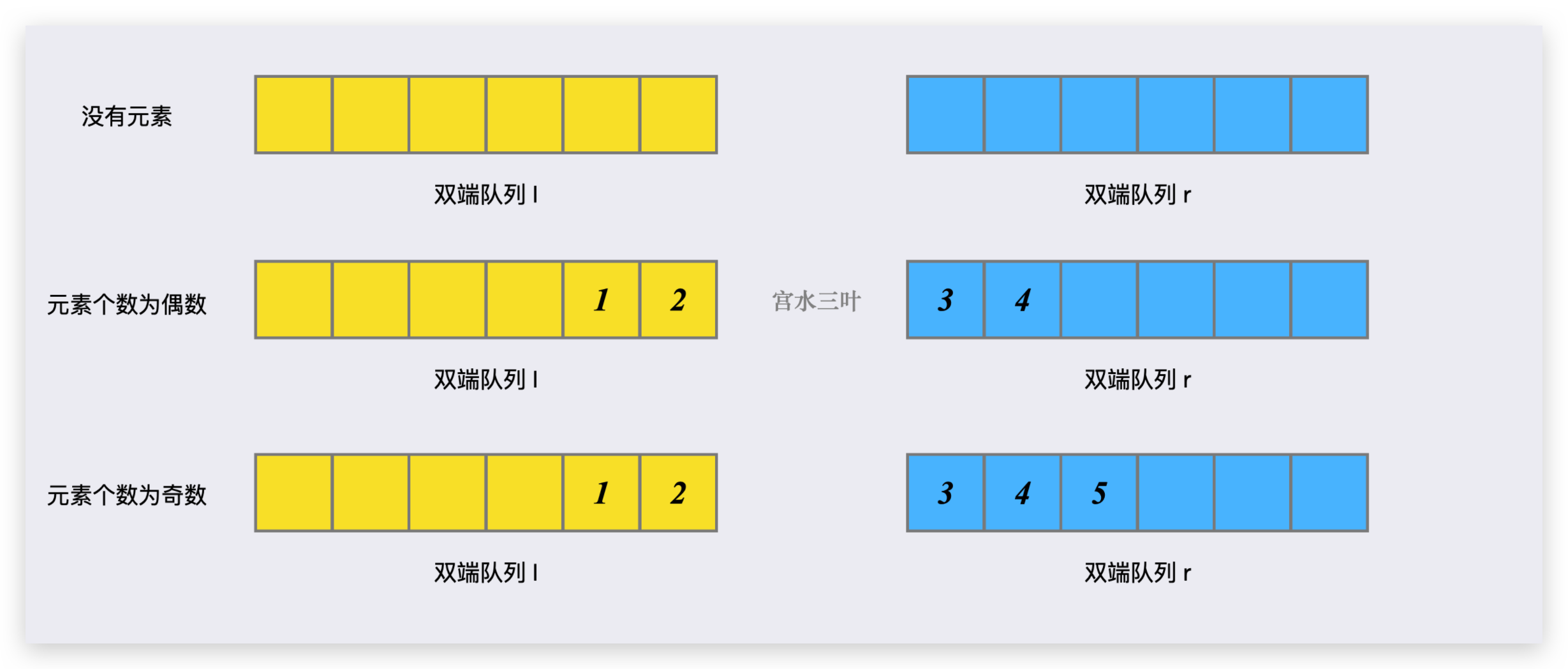
由于双端队列本身支持 $O(1)$ 首尾操作，问题的关键在于如何确保涉及 Middle 操作的高效性。

我们可以设计一个 update 方法，用于确保两队列的相对平衡：

  • 当元素总个数为偶数时，确保两队列元素相等
  • 当元素总个数为奇数时，确保 r 队列比 l 队列元素多一个

如此一来，当我们需要往 Middle 插入元素时，始终往 l 的尾部插入即可；而当需要读取 Middle 位置元素时，根据两队列的元素个数关系决定是从 l 的尾部还是从 r 的头部取元素。

以下是对上述代码中几个操作的简短实现说明：

  • pushFront：将元素添加到 l 队列的头部，调用 update 保持队列平衡
  • pushMiddle：将元素添加到 l 队列的尾部，调用 update 保持队列平衡
  • pushBack：将元素添加到 r 队列的尾部，调用 update 保持队列平衡
  • popFront：若 l 队列不为空，从 l 队列的头部弹出一个元素；否则，从 r 队列的头部弹出一个元素（当且仅当元素个数为 $1$ 时，队列 l 为空，唯一元素在队列 r 中），调用 update 保持队列平衡
  • popMiddle：若 l 队列和 r 队列的大小相等，则从 l 队列的尾部弹出一个元素；否则，从 r 队列的头部弹出一个元素。调用 update 保持队列平衡
  • popBack：从 r 队列的尾部弹出一个元素，调用 update 保持队列平衡

双端队列的实现，可通过「数组 + 首尾坐标指针」来实现。为方便大家理清脉络，先使用语言自带的 Deque 实现一版。

Java 代码（Deque 版）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class FrontMiddleBackQueue {
    Deque<Integer> l = new ArrayDeque<>(1010), r = new ArrayDeque<>(1010);
    public void pushFront(int val) {
        l.addFirst(val);
        update();
    }
    public void pushMiddle(int val) {
        l.addLast(val);
        update();
    }
    public void pushBack(int val) {
        r.addLast(val);
        update();
    }
    public int popFront() {
        if (l.size() + r.size() == 0) return -1;
        int ans = l.size() != 0 ? l.pollFirst() : r.pollFirst();
        update();
        return ans;
    }
    public int popMiddle() {
        if (l.size() + r.size() == 0) return -1;
        int ans = l.size() == r.size() ? l.pollLast() : r.pollFirst();
        update();
        return ans;
    }
    public int popBack() {
        if (l.size() + r.size() == 0) return -1;
        int ans = r.pollLast();
        update();
        return ans;
    }
    void update() {
        while (l.size() > r.size()) r.addFirst(l.pollLast());
        while (r.size() - l.size() > 1) l.addLast(r.pollFirst());
    }
}

看过 Deque 实现版本，考虑如何使用数组实现。

各类操作的总调用次数最多为 $1000$ 次，我们可创建大小为 $2010$ 的数组，并从下标 $1010$（接近中间位置）开始进行存储，这样无论是从前还是往后存数都不会越界。

使用 lhe 和 lta 代表队列 l 的头部和尾部坐标，使用 rhe 和 rta 代表队列 r 的头部和尾部坐标，所有坐标初始值均为 $1100$。

需要注意的是，ta（无论是 lta 还是 rta）是严格指向尾部，因此如果要往尾部插数的话，需要先对指针自增（移到下一个空闲位置），再赋值；而 he（无论是 lhe 还是 rhe）是指向实际队列头部的前一位置，需要先赋值再前移。当 he = ta 代表队列为空。

Java 代码（纯数组版）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class FrontMiddleBackQueue {
    int[] l = new int[2010], r = new int[2010];
    int lhe = 1010, lta = 1010, rhe = 1010, rta = 1010;
    public void pushFront(int val) {
        l[lhe--] = val;
        update();
    }
    public void pushMiddle(int val) {
        l[++lta] = val;
        update();
    }
    public void pushBack(int val) {
        r[++rta] = val;
        update();
    }
    public int popFront() {
        if (getSize(lhe, lta) == 0 && getSize(rhe, rta) == 0) return -1;
        int ans = getSize(lhe, lta) != 0 ? l[++lhe] : r[++rhe];
        update();
        return ans;
    }
    public int popMiddle() {
        if (getSize(lhe, lta) + getSize(rhe, rta) == 0) return -1;
        int ans = getSize(lhe, lta) == getSize(rhe, rta) ? l[lta--] : r[++rhe];
        update();
        return ans;
    }
    public int popBack() {
        if (getSize(lhe, lta) == 0 && getSize(rhe, rta) == 0) return -1;
        int ans = r[rta--];
        update();
        return ans;
    }
    int getSize(int he, int ta) {
        return ta - he;
    }
    void update() {
        while (getSize(lhe, lta) > getSize(rhe, rta)) r[rhe--] = l[lta--];
        while (getSize(rhe, rta) - getSize(lhe, lta) > 1) l[++lta] = r[++rhe];
    }
}

C++ 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class FrontMiddleBackQueue {
public:
    int l[2010], r[2010], lhe = 1010, lta = 1010, rhe = 1010, rta = 1010;
    void pushFront(int val) {
        l[lhe--] = val;
        update();
    }
    void pushMiddle(int val) {
        l[++lta] = val;
        update();
    }
    void pushBack(int val) {
        r[++rta] = val;
        update();
    }
    int popFront() {
        if (getSize(lhe, lta) == 0 && getSize(rhe, rta) == 0) return -1;
        int ans = getSize(lhe, lta) != 0 ? l[++lhe] : r[++rhe];
        update();
        return ans;
    }
    int popMiddle() {
        if (getSize(lhe, lta) == 0 && getSize(rhe, rta) == 0) return -1;
        int ans = getSize(lhe, lta) == getSize(rhe, rta) ? l[lta--] : r[++rhe];
        update();
        return ans;
    }
    int popBack() {
        if (getSize(lhe, lta) == 0 && getSize(rhe, rta) == 0) return -1;
        int ans = r[rta--];
        update();
        return ans;
    }
    int getSize(int he, int ta) {
        return ta - he;
    }
    void update() {
        while (getSize(lhe, lta) > getSize(rhe, rta)) r[rhe--] = l[lta--];
        while (getSize(rhe, rta) - getSize(lhe, lta) > 1) l[++lta] = r[++rhe];
    }
};

Python 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class FrontMiddleBackQueue:
    def __init__(self):
        self.l, self.r = [0] * 2010, [0] * 2010
        self.r = [0] * 2010
        self.lhe, self.lta, self.rhe, self.rta = 1010, 1010, 1010, 1010

    def pushFront(self, val: int) -> None:
        self.l[self.lhe] = val
        self.lhe -= 1
        self.update()

    def pushMiddle(self, val: int) -> None:
        self.lta += 1
        self.l[self.lta] = val
        self.update()

    def pushBack(self, val: int) -> None:
        self.rta += 1
        self.r[self.rta] = val
        self.update()

    def popFront(self) -> int:
        if self.getSize(self.lhe, self.lta) + self.getSize(self.rhe, self.rta) == 0:
            return -1
        if self.getSize(self.lhe, self.lta) != 0:
            self.lhe += 1
            ans = self.l[self.lhe]
        else:
            self.rhe += 1
            ans = self.r[self.rhe]
        self.update()
        return ans

    def popMiddle(self) -> int:
        if self.getSize(self.lhe, self.lta) + self.getSize(self.rhe, self.rta) == 0:
            return -1
        if self.getSize(self.lhe, self.lta) == self.getSize(self.rhe, self.rta):
            ans = self.l[self.lta]
            self.lta -= 1
        else:
            self.rhe += 1
            ans = self.r[self.rhe]
        self.update()
        return ans

    def popBack(self) -> int:
        if self.getSize(self.lhe, self.lta) + self.getSize(self.rhe, self.rta) == 0:
            return -1
        ans = self.r[self.rta]
        self.rta -= 1
        self.update()
        return ans

    def getSize(self, he: int, ta: int) -> int:
        return ta - he

    def update(self) -> None:
        while self.getSize(self.lhe, self.lta) > self.getSize(self.rhe, self.rta):
            self.r[self.rhe] = self.l[self.lta]
            self.rhe -= 1
            self.lta -= 1
        while self.getSize(self.rhe, self.rta) - self.getSize(self.lhe, self.lta) > 1:
            self.lta += 1
            self.rhe += 1
            self.l[self.lta] = self.r[self.rhe]

TypeScript 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class FrontMiddleBackQueue {
    private l: number[];
    private r: number[];
    private lhe: number;
    private lta: number;
    private rhe: number;
    private rta: number;
    constructor() {
        this.l = Array(2010).fill(0), this.r = Array(2010).fill(0);
        this.lhe = 1010, this.lta = 1010, this.rhe = 1010, this.rta = 1010;
    }
    pushFront(val: number): void {
        this.l[this.lhe--] = val;
        this.update();
    }
    pushMiddle(val: number): void {
        this.l[++this.lta] = val;
        this.update();
    }
    pushBack(val: number): void {
        this.r[++this.rta] = val;
        this.update();
    }
    popFront(): number {
        if (this.getSize(this.lhe, this.lta) + this.getSize(this.rhe, this.rta) == 0) return -1;
        const ans = this.getSize(this.lhe, this.lta) != 0 ? this.l[++this.lhe] : this.r[++this.rhe];
        this.update();
        return ans;
    }
    popMiddle(): number {
        if (this.getSize(this.lhe, this.lta) + this.getSize(this.rhe, this.rta) == 0) return -1;
        const ans = this.getSize(this.lhe, this.lta) == this.getSize(this.rhe, this.rta) ? this.l[this.lta--] : this.r[++this.rhe];
        this.update();
        return ans;
    }
    popBack(): number {
        if (this.getSize(this.lhe, this.lta) + this.getSize(this.rhe, this.rta) == 0) return -1;
        const ans = this.r[this.rta--];
        this.update();
        return ans;
    }
    private getSize(he: number, ta: number): number {
        return ta - he;
    }
    private update(): void {
        while (this.getSize(this.lhe, this.lta) > this.getSize(this.rhe, this.rta)) this.r[this.rhe--] = this.l[this.lta--];
        while (this.getSize(this.rhe, this.rta) - this.getSize(this.lhe, this.lta) > 1) this.l[++this.lta] = this.r[++this.rhe];
    }
}

  • 时间复杂度：所有操作复杂度均为 $O(1)$
  • 空间复杂度：$O(n)$

进阶

更进一步，使用双向链表并与实现 update 类似效果，维护 Middle 位置的元素节点，同样可实现 $O(1)$ 各项操作，你能完成吗？

与纯数组版相比，使用链表好处在于可严格按需创建。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
class Node {
    Node prev, next;
    int val;
    Node (int _val) {
        val = _val;
    }
}
class FrontMiddleBackQueue {
    Node he, ta, mid;
    int lsz, rsz;
    public FrontMiddleBackQueue() {
        he = new Node(-1); ta = new Node(-1);
        he.next = ta; ta.prev = he;
        mid = ta;
        lsz = rsz = 0;
    }
    public void pushFront(int val) {
        Node cur = new Node(val);
        cur.next = he.next;
        cur.prev = he;
        he.next.prev = cur;
        he.next = cur;
        lsz++;
        update();
    }
    public void pushMiddle(int val) {
        Node cur = new Node(val);
        cur.next = mid;
        cur.prev = mid.prev;
        mid.prev.next = cur;
        mid.prev = cur;
        lsz++;
        update();
    }
    public void pushBack(int val) {
        Node cur = new Node(val);
        cur.next = ta;
        cur.prev = ta.prev;
        ta.prev.next = cur;
        ta.prev = cur;
        rsz++;
        update();
    }
    public int popFront() {
        if (lsz + rsz == 0) return -1;
        int ans = he.next.val;
        he.next.next.prev = he;
        he.next = he.next.next;
        lsz--;
        update();
        return ans;
    }
    public int popMiddle() {
        if (lsz + rsz == 0) return -1;
        Node realMid = null;
        if (lsz == rsz) {
            realMid = mid.prev;
            lsz--;
        } else {
            realMid = mid;
            mid = mid.next;
            rsz--;
        }
        int ans = realMid.val;
        realMid.prev.next = realMid.next;
        realMid.next.prev = realMid.prev;
        realMid = realMid.next;
        update();
        return ans;
    }
    public int popBack() {
        if (lsz + rsz == 0) return -1;
        int ans = ta.prev.val;
        ta.prev.prev.next = ta;
        ta.prev = ta.prev.prev;
        rsz--;
        update();
        return ans;
    }
    void update() {
        while (lsz > rsz) {
            mid = mid.prev;
            lsz--; rsz++;
        }
        while (rsz - lsz > 1) {
            mid = mid.next;
            lsz++; rsz--;
        }
        if (lsz + rsz == 1) mid = ta.prev;
        if (lsz + rsz == 0) mid = ta;
    }
}

最后

这是我们「刷穿 LeetCode」系列文章的第 No.1670 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。