LC 662. 二叉树最大宽度
题目描述
这是 LeetCode 上的 662. 二叉树最大宽度 ,难度为 中等。
给你一棵二叉树的根节点 root,返回树的最大宽度。
树的「最大宽度」是所有层中最大的宽度 。
每一层的宽度被定义为该层最左和最右的非空节点(即两个端点)之间的长度。
将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
示例 1: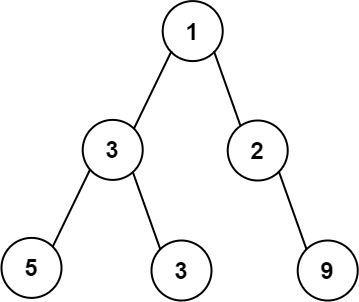
1
2
3
4
5输入:root = [1,3,2,5,3,null,9]
输出:4
解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。
示例 2: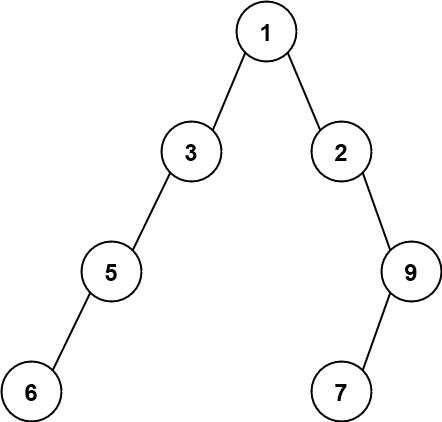
1
2
3
4
5输入:root = [1,3,2,5,null,null,9,6,null,7]
输出:7
解释:最大宽度出现在树的第 4 层,宽度为 7 (6,null,null,null,null,null,7) 。
示例 3: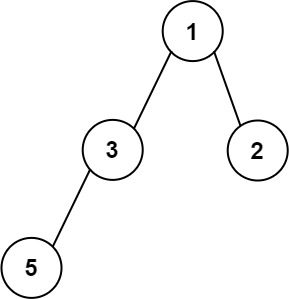
1
2
3
4
5输入:root = [1,3,2,5]
输出:2
解释:最大宽度出现在树的第 2 层,宽度为 2 (3,2) 。
提示:
- 树中节点的数目范围是 $[1, 3000]$
- $-100 <= Node.val <= 100$
DFS
根据满二叉树的节点编号规则:若根节点编号为 u,则其左子节点编号为 u << 1,其右节点编号为 u << 1 | 1。
一个朴素的想法是:我们在 DFS过程中使用两个哈希表分别记录每层深度中的最小节点编号和最大节点编号,两者距离即是当前层的宽度,最终所有层数中的最大宽度即是答案。
而实现上,我们可以利用先 DFS 左节点,再 DFS 右节点的性质可知,每层的最左节点必然是最先被遍历到,因此我们只需要记录当前层最先被遍历到点编号(即当前层最小节点编号),并在 DFS 过程中计算宽度,更新答案即可。
看到评论区有同学讨论关于编号溢出问题,之所以溢出仍能
AC是因为测试数组中没有同层内「宽度」左端点不溢出,右端点溢出,同时该层就是最大宽度的数据点。
我们可以通过u = u - map.get(depth) + 1操作来对同层内的节点进行重新编号(使得同层最靠左的非空节点编号为 $1$)。
通过重编号操作 我们可以消除由于深度加深带来的编号溢出问题,同时TS代码不再需要使用bigint。
Java 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
Map<Integer, Integer> map = new HashMap<>();
int ans;
public int widthOfBinaryTree(TreeNode root) {
dfs(root, 1, 0);
return ans;
}
void dfs(TreeNode root, int u, int depth) {
if (root == null) return ;
if (!map.containsKey(depth)) map.put(depth, u);
ans = Math.max(ans, u - map.get(depth) + 1);
u = u - map.get(depth) + 1;
dfs(root.left, u << 1, depth + 1);
dfs(root.right, u << 1 | 1, depth + 1);
}
}
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
unordered_map<int, int> map;
int ans = 0;
int widthOfBinaryTree(TreeNode* root) {
dfs(root, 1, 0);
return ans;
}
void dfs(TreeNode* root, int u, int depth) {
if (!root) return;
if (!map.count(depth)) map[depth] = u;
ans = max(ans, u - map[depth] + 1);
u = u - map[depth] + 1;
dfs(root->left, u << 1, depth + 1);
dfs(root->right, u << 1 | 1, depth + 1);
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution:
def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
mapping = {}
ans = 0
def dfs(root, u, depth):
nonlocal ans
if not root:
return
if depth not in mapping:
mapping[depth] = u
ans = max(ans, u - mapping[depth] + 1)
u = u - mapping[depth] + 1
dfs(root.left, u << 1, depth + 1)
dfs(root.right, u << 1 | 1, depth + 1)
dfs(root, 1, 0)
return ans
TypeScript 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16let map = new Map<number, number>()
let ans = 0
function widthOfBinaryTree(root: TreeNode | null): number {
map.clear()
ans = 0
dfs(root, 1, 0)
return ans
};
function dfs(root: TreeNode | null, u: number, depth: number): void {
if (root == null) return
if (!map.has(depth)) map.set(depth, u)
ans = Math.max(ans, u - map.get(depth) + 1)
u = u - map.get(depth) + 1
dfs(root.left, u << 1, depth + 1)
dfs(root.right, u << 1 | 1, depth + 1)
}
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.662 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
