LC 406. 根据身高重建队列

题目描述

这是 LeetCode 上的 406. 根据身高重建队列 ，难度为 中等。

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 $people[i] = [h_i, k_i]$ 表示第 $i$ 个人的身高为 $h_i$ ，前面 正好 有 $k_i$ 个身高大于或等于 $h_i$ 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 $queue[j] = [h_j, k_j]$ 是队列中第 $j$ 个人的属性（$queue[0]$ 是排在队列前面的人）。

示例 1：

输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]

输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

示例 2：

输入：people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]

输出：[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]

提示：

• $1 <= people.length <= 2000$
• $0 <= h_i <= 10^6$
• $0 <= k_i < people.length$
• 题目数据确保队列可以被重建

---

构造 + 二分 + 树状数组

这是一道非常综合的题目。

首先根据双关键字排序：当「高度（第一维）」不同，根据高度排升序，对于高度相同的情况，则根据「编号（第二维）」排降序。

采取这样的排序规则的好处在于：在从前往后处理某个 $people[i]$ 时，我们可以直接将其放置在「当前空位序列（从左往后统计的，不算已被放置的位置）」中的 $people[i][1] + 1$ 位（预留了前面的 $people[i][1]$ 个位置给后面的数）。

关于「空位序列」如图所示（黄色代表已被占用，白色代表尚未占用）：

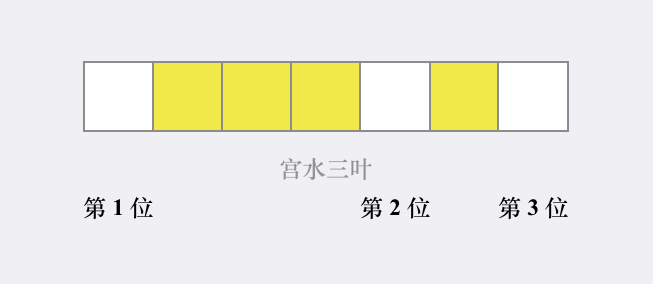
具体的，我们按照构造的合理性来解释双关键字排序的合理性，假设当前处理的是 $people[i]$：

根据「高度」排升序，根据「编号」排降序：由于首先是根据「高度」排升序，因此当 $people[i]$ 被放置在「当前空位序列」的第 $people[i][1] + 1$ 之后，无论后面的 $people[j]$ 如何放置，都不会影响 $people[i]$ 的合法性：后面的数的高度都不低于 $people[i][0]$，无论放在 $people[i][1] + 1$ 前面还是后面都不会影响 $people[i]$ 的合法性。

同时对于高度（第一维）相同，编号（第二维）不同的情况，我们进行了「降序」处理，因此「每次将 $people[i]$ 放置在空白序列的 $people[i][1] + 1$ 位置的」的逻辑能够沿用。即 对于「高度」相同「编号」不同的情况，会被按照「从右到左」依次放置，导致了每个 $people[i]$ 被放置时，都不会受到「高度」相同的其他 $people[j]$ 所影响。换句话说，当 $people[i]$ 放置时，其左边必然不存在其他高度为 $people[i][0]$ 的成员。

剩下的在于，如何快速找到「空白序列中的第 $k$ 个位置」，这可以通过「二分 + 树状数组」来做。

对于已被使用的位置标记为 $1$，未使用的位置为 $0$，那么第一个满足「$0$ 的个数大于等于 $k + 1$」的位置即是目标位置，在长度明确的情况下，求 $0$ 的个数和求 $1$ 的个数等同，对于位置 $x$ 而言（下标从 $1$ 开始，总个数为 $x$），如果在 $[1, x]$ 范围内有 $k + 1$ 个 $0$，等价于有 $x - (k + 1)$ 个 $1$，求解 $[1, x]$ 范围内 $1$ 的个数等价于求前缀和，即区间查询，同时我们每次使用一个新的位置后 ，需要对其进行标记，涉及单点修改，使用「树状数组」求解。

代码：

class Solution {
    int n;
    int[] tr;
    int lowbit(int x) {
        return x & -x;
    }
    void add(int x, int v) {
        for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
    }
    int query(int x) {
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) ans += tr[i];
        return ans;
    }
    public int[][] reconstructQueue(int[][] ps) {
        Arrays.sort(ps, (a, b)->{
            if (a[0] != b[0]) return a[0] - b[0];
            return b[1] - a[1];
        });
        n = ps.length;
        tr = new int[n + 1];
        int[][] ans = new int[n][2];
        for (int[] p : ps) {
            int h = p[0], k = p[1];
            int l = 1, r = n;
            while (l < r) {
                int mid = l + r >> 1;
                if (mid - query(mid) >= k + 1) r = mid;
                else l = mid + 1;
            }
            ans[r - 1] = p;
            add(r, 1);
        }
        return ans;
    }
}

• 时间复杂度：排序的复杂度为 $O(n\log{n})$；共要处理 $n$ 个 $people[i]$，每次处理需要二分，复杂度为 $O(\log{n})$；每次二分和找到答案后需要操作树状数组，复杂度为 $O(\log{n})$。整体复杂度为 $O(n \times \log{n} \times \log{n})$
• 空间复杂度：$O(n)$

---

最后

这是我们「刷穿 LeetCode」系列文章的第 No.406 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。