LC 1728. 猫和老鼠 II
题目描述
这是 LeetCode 上的 1728. 猫和老鼠 II ,难度为 困难。
一只猫和一只老鼠在玩一个叫做猫和老鼠的游戏。
它们所处的环境设定是一个 rows x cols 的方格 grid ,其中每个格子可能是一堵墙、一块地板、一位玩家(猫或者老鼠)或者食物。
- 玩家由字符
'C'(代表猫)和'M'(代表老鼠)表示。 - 地板由字符
'.'表示,玩家可以通过这个格子。 - 墙用字符
'#'表示,玩家不能通过这个格子。 - 食物用字符
'F'表示,玩家可以通过这个格子。 - 字符
'C','M'和'F'在grid中都只会出现一次。
猫和老鼠按照如下规则移动:
- 老鼠 先移动 ,然后两名玩家轮流移动。
- 每一次操作时,猫和老鼠可以跳到上下左右四个方向之一的格子,他们不能跳过墙也不能跳出 grid 。
catJump和mouseJump是猫和老鼠分别跳一次能到达的最远距离,它们也可以跳小于最大距离的长度。- 它们可以停留在原地。
- 老鼠可以跳跃过猫的位置。
游戏有 $4$ 种方式会结束:
- 如果猫跟老鼠处在相同的位置,那么猫获胜。
- 如果猫先到达食物,那么猫获胜。
- 如果老鼠先到达食物,那么老鼠获胜。
- 如果老鼠不能在 $1000$ 次操作以内到达食物,那么猫获胜。
给你 rows x cols 的矩阵 grid 和两个整数 catJump 和 mouseJump,双方都采取最优策略,如果老鼠获胜,那么请你返回 true,否则返回 false。
示例 1: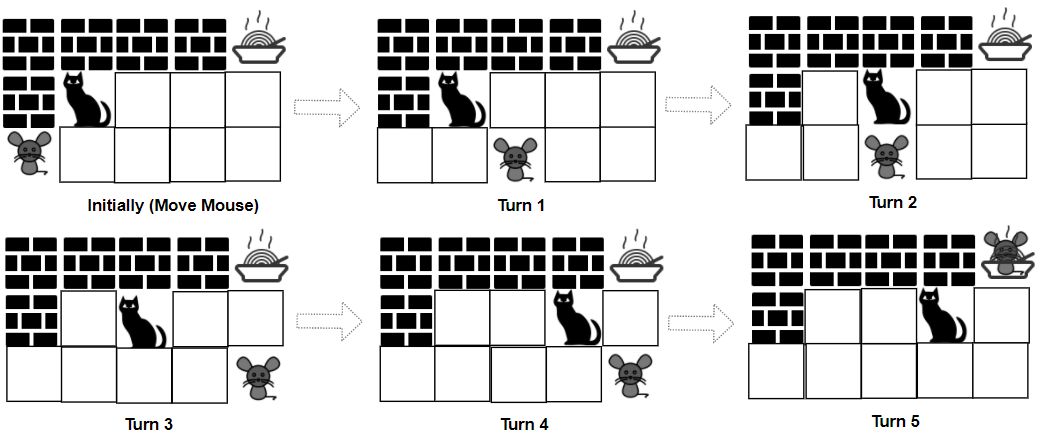
1
2
3
4
5输入:grid = ["####F","#C...","M...."], catJump = 1, mouseJump = 2
输出:true
解释:猫无法抓到老鼠,也没法比老鼠先到达食物。
示例 2: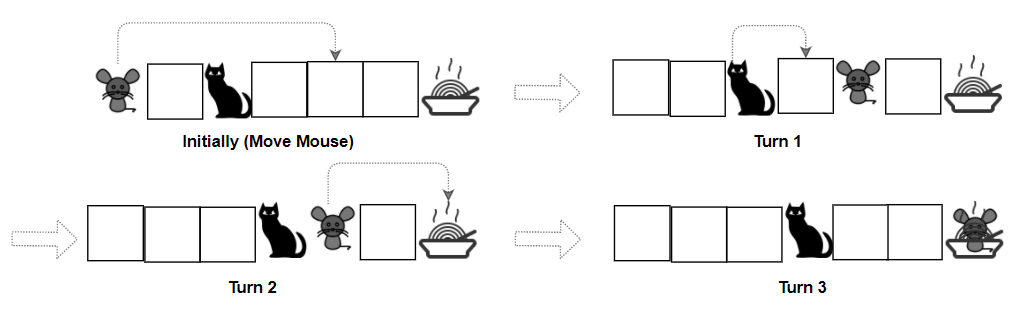
1
2
3输入:grid = ["M.C...F"], catJump = 1, mouseJump = 4
输出:true
示例 3:1
2
3输入:grid = ["M.C...F"], catJump = 1, mouseJump = 3
输出:false
示例 4:1
2
3输入:grid = ["C...#","...#F","....#","M...."], catJump = 2, mouseJump = 5
输出:false
示例 5:1
2
3输入:grid = [".M...","..#..","#..#.","C#.#.","...#F"], catJump = 3, mouseJump = 1
输出:true
提示:
- $rows == grid.length$
- $cols = grid[i].length$
- $1 <= rows, cols <= 8$
- $grid[i][j]$ 只包含字符
'C','M','F','.'和'#'。 grid中只包含一个'C','M'和'F'。- $1 <= catJump, mouseJump <= 8$
博弈论 DP
当时在 (题解) 913. 猫和老鼠 没能证出来更小 $K$ 值(回合数)的正确性,用的 $2n^2$ 做的 ,其余题解说 $2 n$ 合法,后来也被证实是错误的。
对于本题如果用相同的分析思路,状态数多达 $8 \times 8 \times 8 \times 8 \times 2 = 8192$ 种,题目很贴心调整了规则为 $1000$ 步以内为猫获胜,但证明 $K$ 的理论上界仍是困难(上次分析不出来,这次压根不想分析
如果忽略 $K$ 值分析,代码还是很好写的:定义函数 int dfs(int x, int y, int p, int q, int k) 并配合记忆化搜索,其中鼠位于 $(x, y)$,猫位于 $(p, q)$,当前轮数为 $k$(由 $k$ 的奇偶性可知是谁的回合)。
对边界情况进行讨论,移动过程中按照规则进行(四联通,移动最大距离为 mouseJump 和 catJump),注意一旦遇到边界或者墙就要截断。
Java 使用静态数组,用一个 int 代表双方所在位置,最大回合数 $K = 1000$,2022-05-10 可以过。这道题给的时间上限很高,我调整为 $K = 1500$ 跑成 $2.5s$ 也可以过。本来想要加个卡常,每 $200$ 轮检查一下运行总时长,尽量将时间压在 $850ms$ 以内,现在看来好像用不到。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56import java.time.Clock;
class Solution {
static int S = 8 * 8 * 8 * 8, K = 1000;
static int[][] f = new int[S][K]; // mouse : 0 / cat : 1
String[] g;
int n, m, a, b, tx, ty;
int[][] dirs = new int[][]{{1,0}, {-1,0}, {0,1}, {0,-1}};
// mouse : (x, y) / cat : (p, q)
int dfs(int x, int y, int p, int q, int k) {
int state = (x << 9) | (y << 6) | (p << 3) | q;
if (k == K - 1) return f[state][k] = 1;
if (x == p && y == q) return f[state][k] = 1;
if (x == tx && y == ty) return f[state][k] = 0;
if (p == tx && q == ty) return f[state][k] = 1;
if (f[state][k] != -1) return f[state][k];
if (k % 2 == 0) { // mouse
for (int[] di : dirs) {
for (int i = 0; i <= b; i++) {
int nx = x + di[0] * i, ny = y + di[1] * i;
if (nx < 0 || nx >= n || ny < 0 || ny >= m) break;
if (g[nx].charAt(ny) == '#') break;
if (dfs(nx, ny, p, q, k + 1) == 0) return f[state][k] = 0;
}
}
return f[state][k] = 1;
} else { // cat
for (int[] di : dirs) {
for (int i = 0; i <= a; i++) {
int np = p + di[0] * i, nq = q + di[1] * i;
if (np < 0 || np >= n || nq < 0 || nq >= m) break;
if (g[np].charAt(nq) == '#') break;
if (dfs(x, y, np, nq, k + 1) == 1) return f[state][k] = 1;
}
}
return f[state][k] = 0;
}
}
public boolean canMouseWin(String[] grid, int catJump, int mouseJump) {
g = grid;
n = g.length; m = g[0].length(); a = catJump; b = mouseJump;
for (int i = 0; i < S; i++) Arrays.fill(f[i], -1);
int x = 0, y = 0, p = 0, q = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (g[i].charAt(j) == 'M') {
x = i; y = j;
} else if (g[i].charAt(j) == 'C') {
p = i; q = j;
} else if (g[i].charAt(j) == 'F') {
tx = i; ty = j;
}
}
}
return dfs(x, y, p, q, 0) == 0;
}
}
- 时间复杂度:令 $n$ 和 $m$ 分别为矩阵的长宽,最长移动距离为 $L$,复杂度为 $O(n^2 \times m^2 \times 1000 \times 4 \times L)$
- 空间复杂度:$O(n^2 \times m^2 \times 1000)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.1728 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
