LC 1801. 积压订单中的订单总数

题目描述

这是 LeetCode 上的 1801. 积压订单中的订单总数 ，难度为 中等。

给你一个二维整数数组 $orders$ ，其中每个 $orders[i] = [price_i, amount_i, orderType_i]$ 表示有 $amount_i$ 笔类型为 $orderType_i$、价格为 $price_i$ 的订单。

订单类型 $orderType_i$ 可以分为两种：

  • $0$ 表示这是一批采购订单 buy
  • $1$ 表示这是一批销售订单 sell

注意，$orders[i]$ 表示一批共计 $amount_i$ 笔的独立订单，这些订单的价格和类型相同。

对于所有有效的 $i$ ，由 $orders[i]$ 表示的所有订单提交时间均早于 $orders[i+1]$ 表示的所有订单。

存在由未执行订单组成的积压订单。积压订单最初是空的。

提交订单时，会发生以下情况：

  • 如果该订单是一采购订单 buy，则可以查看积压订单中价格 最低 的销售订单 sell。如果该销售订单 sell 的价格 低于或等于 当前采购订单 buy 的价格，则匹配并执行这两笔订单，并将销售订单 sell 从积压订单中删除。否则，采购订单 buy 将会添加到积压订单中。
  • 反之亦然，如果该订单是一笔销售订单 sell，则可以查看积压订单中价格 最高 的采购订单 buy。如果该采购订单 buy 的价格 高于或等于 当前销售订单 sell 的价格，则匹配并执行这两笔订单，并将采购订单 buy 从积压订单中删除。否则，销售订单 sell 将会添加到积压订单中。

输入所有订单后，返回积压订单中的订单总数。

由于数字可能很大，所以需要返回对 $10^9 + 7$ 取余的结果。

示例 1：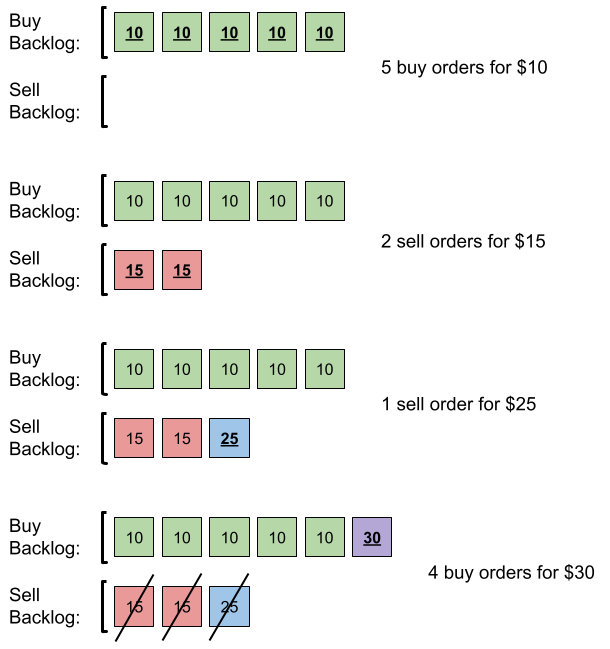

1
2
3
4
5
6
7
8
9
10
输入：orders = [[10,5,0],[15,2,1],[25,1,1],[30,4,0]]

输出：6

解释：输入订单后会发生下述情况：
- 提交 5 笔采购订单，价格为 10 。没有销售订单，所以这 5 笔订单添加到积压订单中。
- 提交 2 笔销售订单，价格为 15 。没有采购订单的价格大于或等于 15 ，所以这 2 笔订单添加到积压订单中。
- 提交 1 笔销售订单，价格为 25 。没有采购订单的价格大于或等于 25 ，所以这 1 笔订单添加到积压订单中。
- 提交 4 笔采购订单，价格为 30 。前 2 笔采购订单与价格最低（价格为 15）的 2 笔销售订单匹配，从积压订单中删除这 2 笔销售订单。第 3 笔采购订单与价格最低的 1 笔销售订单匹配，销售订单价格为 25 ，从积压订单中删除这 1 笔销售订单。积压订单中不存在更多销售订单，所以第 4 笔采购订单需要添加到积压订单中。
最终，积压订单中有 5 笔价格为 10 的采购订单，和 1 笔价格为 30 的采购订单。所以积压订单中的订单总数为 6 。

示例 2：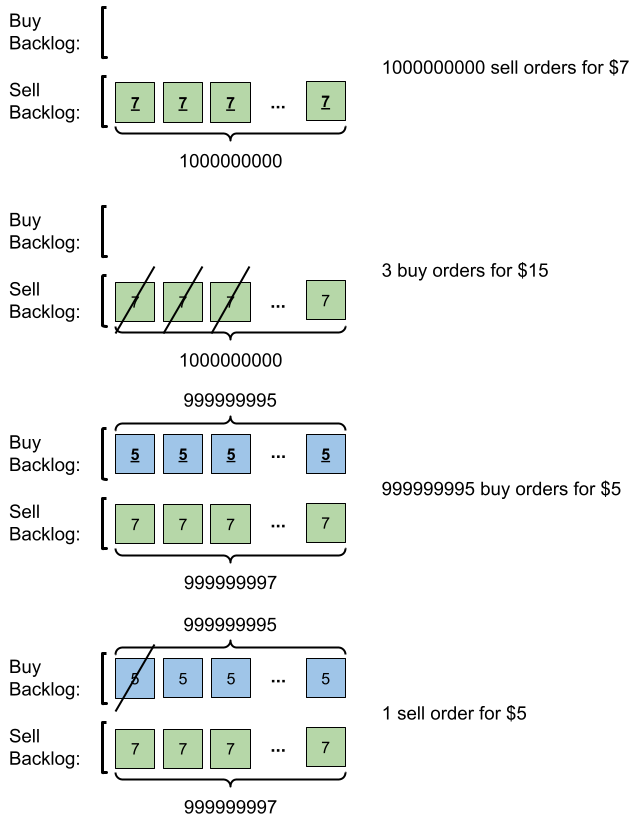

1
2
3
4
5
6
7
8
9
10
输入：orders = [[7,1000000000,1],[15,3,0],[5,999999995,0],[5,1,1]]

输出：999999984

解释：输入订单后会发生下述情况：
- 提交 109 笔销售订单，价格为 7 。没有采购订单，所以这 109 笔订单添加到积压订单中。
- 提交 3 笔采购订单，价格为 15 。这些采购订单与价格最低（价格为 7 ）的 3 笔销售订单匹配，从积压订单中删除这 3 笔销售订单。
- 提交 999999995 笔采购订单，价格为 5 。销售订单的最低价为 7 ，所以这 999999995 笔订单添加到积压订单中。
- 提交 1 笔销售订单，价格为 5 。这笔销售订单与价格最高（价格为 5 ）的 1 笔采购订单匹配，从积压订单中删除这 1 笔采购订单。
最终，积压订单中有 (1000000000-3) 笔价格为 7 的销售订单，和 (999999995-1) 笔价格为 5 的采购订单。所以积压订单中的订单总数为 1999999991 ，等于 999999984 % (109 + 7) 。

提示：

  • $1 <= orders.length <= 10^5$
  • $orders[i].length == 3$
  • $1 <= pricei, amounti <= 10^9$
  • orderTypei 为 $0$ 或 $1$

模拟 + 数据结构

整理题意：从前往后处理所有的 $orders[i]$，对于 buy 类型的订单，从积压订单中找价格低于等于当前价格的 sell 订单进行抵消；同理，对于 sell 类型的订单，从积压订单中找价格高于等于当前价格的 buy 订单进行抵消。问最终有多少积压订单。

这个找「最低/最高」价格的操作可以利用优先队列（堆）来做，对于积压的 buy 类型订单，我们总是要找价格高的，使用大根堆维护；对于积压的 sell 类型订单，我们总是要找价格低的，使用小根堆维护。

两个优先队列（堆）均维护形如 $(price_i, amount_i)$ 的二元组信息，代表价格为 $price_i$ 的订单积压了 $amount_i$ 单。

当处理（尝试匹配）了所有的 $orders[i]$ 之后，统计两个优先队列（堆）中订单数量即是答案。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int getNumberOfBacklogOrders(int[][] orders) {
        PriorityQueue<int[]> buy = new PriorityQueue<>((a,b)->b[0]-a[0]), sell = new PriorityQueue<>((a,b)->a[0]-b[0]);
        PriorityQueue<int[]> from = null, to = null;
        boolean fromIsSell = false;
        for (int[] order : orders) {
            int p = order[0], a = order[1], t = order[2];
            if (t == 0) {
                from = sell; to = buy; fromIsSell = true;
            } else {
                from = buy; to = sell; fromIsSell = false;
            }
            while (a > 0 && !from.isEmpty() && (fromIsSell ? from.peek()[0] <= p : from.peek()[0] >= p)) {
                int[] cur = from.poll();
                int cnt = Math.min(cur[1], a);
                cur[1] -= cnt; a -= cnt;
                if (cur[1] > 0) from.add(cur);
            }
            if (a > 0) to.add(new int[]{p, a});
        }
        int ans = 0;
        for (PriorityQueue<int[]> q : new PriorityQueue[]{buy, sell}) {
            while (!q.isEmpty()) {
                ans += q.poll()[1];
                ans %= (int)1e9+7;
            }
        }
        return ans;
    }
}

-

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:
        buy, sell = [], []
        for p, a, t in orders:
            if t == 0:
                from_heap, to_heap, from_is_sell = sell, buy, True
            else:
                from_heap, to_heap, from_is_sell = buy, sell, False
            while a and from_heap and (from_heap[0][0] <= p if from_is_sell else -from_heap[0][0] >= p):
                cur = heapq.heappop(from_heap)
                if cur[1] > a:
                    heapq.heappush(from_heap, (cur[0], cur[1] - a))
                    a = 0
                else:
                    a -= cur[1]
            if a:
                heapq.heappush(to_heap, (-p if from_is_sell else p, a))
        ans, mod = 0, int(1e9)+7
        for _, a in buy + sell:
            ans += a
        return ans % mod

  • 时间复杂度：令$n$ 为数组 orders 的长度，复杂度为 $O(n\log{n})$
  • 空间复杂度：$O(n)$

最后

这是我们「刷穿 LeetCode」系列文章的第 No.1801 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。