LC 1719. 重构一棵树的方案数
题目描述
这是 LeetCode 上的 1719. 重构一棵树的方案数 ,难度为 困难。
给你一个数组 pairs,其中 $pairs[i] = [x_i, y_i]$ ,并且满足:
pairs中没有重复元素- $x_i < y_i$
令 ways 为满足下面条件的有根树的方案数:
- 树所包含的所有节点值都在
pairs中。 - 一个数对 $[x_i, y_i]$ 出现在
pairs中 当且仅当 $x_i$ 是 $y_i$ 的祖先或者 $y_i$ 是 $x_i$ 的祖先。 - 注意:构造出来的树不一定是二叉树。
两棵树被视为不同的方案当存在至少一个节点在两棵树中有不同的父节点。
请你返回:
- 如果 ways == 0 ,返回 0 。
- 如果 ways == 1 ,返回 1 。
- 如果 ways > 1 ,返回 2 。
一棵 有根树 指的是只有一个根节点的树,所有边都是从根往外的方向。
我们称从根到一个节点路径上的任意一个节点(除去节点本身)都是该节点的 祖先 。根节点没有祖先。
示例 1: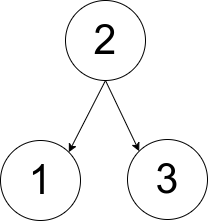
1
2
3
4
5输入:pairs = [[1,2],[2,3]]
输出:1
解释:如上图所示,有且只有一个符合规定的有根树。
示例 2:
1
2
3
4
5输入:pairs = [[1,2],[2,3],[1,3]]
输出:2
解释:有多个符合规定的有根树,其中三个如上图所示。
示例 3:1
2
3
4
5输入:pairs = [[1,2],[2,3],[2,4],[1,5]]
输出:0
解释:没有符合规定的有根树。
提示:
- $1 <= pairs.length <= 10^5$
- $1 <= xi < yi <= 500$
pairs中的元素互不相同。
构造 + 验证(合法性 + 非唯一性)
这道题是名副其实的困难题,我最早的提交时间是去年 $3$ 月,起初只能想到 $O(n * m)$ 的做法,对于一颗多叉树来说显然会 TLE,虽然到现在印象不深了,但如果不是之前做过,今天大概率会很晚才能发布题解。
该题突破口在于如何利用 pairs 构造出一种具体方案,然后辨别方案的合法性(是否返回 $0$)和方案中的某些点是否可相互替换(返回 $1$ 还是 $2$)。
给定 pairs 数组为父子关系,对于 $pairs[i] = (a,b)$ 而言,既可以是 $a$ 为 $b$ 祖宗节点,也可以是 $b$ 为 $a$ 祖宗节点。
题目的「当且仅当」含义为所有的 pairs 在具体方案中均有体现,因此先考虑如何使用 pairs 构造出具体方案。
如果使用一棵合法树而言:每个子树的根节点在 pairs 中的出现数量满足大于等于其子节点在 pairs 中出现的数量(当某个根节点只有一个子节点时可取等号)。
利用此性质,虽然我们无法得知某个 $pairs[i]$ 真实的父子关系,但统计每个点的「度数」可以作为决策根节点的依据。
具体的,遍历 pairs 并统计所有点的度数,同时为了后续构造可以快速查询某两个点是否为父子关系,使用邻接矩阵 $g$ 存储关系,并使用 Set 统计点集。
之后将点按照「度数」降序,从前往后处理每个点,尝试构建具体方案(第一个点作为具体方案的根节点)。
对于每个非根节点 $a$ 而言,按道理我们可以将其添加到任意一个「度数不小于 $cnt[i]$」且「与其存在父子关系的」$b$ 中,但这样构造方式,只能确保能够得到「合法性」的结果,会为对于后续的「非唯一性」验证带来巨大困难。
因此这里尝试构造的关键点在于:我们为 $a$ 找 $b$ 的时候,应当找符合条件的、度数与 $a$ 相近的点。由于我们已经提前根据「度数」进行降序,这个找最优点的操作可从 $a$ 所在位置开始进行往回找,找到第一个满足「与 $a$ 存在父子关系」的点 $b$ 作为具体方案中 $a$ 的根节点。
这样的构造逻辑为后续的「非唯一性」验证带来的好处是:如果存在多个点能够相互交换位置的话,其在具体方案中必然为直接的父子关系,即我们能够通过判断 $cnts[i]$ 和 $cnts[fa[i]]$ 是否相等,来得知在具体方案中点 $i$ 和 $fa[i]$ 能够交换,并且如果能够交换,具体方案的合法性不会发生改变。
一些细节:
pairs的数据范围为 $10^4$,而后续的尝试构造,最坏情况下点数也在这个数量级上,为了防止在复杂度为 $O(n^2)$ 的尝试构造上耗费大量时间,可以增加 $m < n - 1$ 的判断,在点数为 $n$ 的情况下,父子关系的最小值为 $n - 1$,当且仅当有一个根节点,其余均为叶子节点时取得,因此如果父子关系数量小于 $n - 1$,必然不为单棵子树,而是森林。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution {
int N = 510;
int[] cnts = new int[N], fa = new int[N];
boolean[][] g = new boolean[N][N];
public int checkWays(int[][] pairs) {
int m = pairs.length;
Set<Integer> set = new HashSet<>();
for (int[] p : pairs) {
int a = p[0], b = p[1];
g[a][b] = g[b][a] = true;
cnts[a]++; cnts[b]++;
set.add(a); set.add(b);
}
List<Integer> list = new ArrayList<>(set);
Collections.sort(list, (a,b)->cnts[b]-cnts[a]);
int n = list.size(), root = list.get(0);
if (m < n - 1) return 0; // 森林
fa[root] = -1;
for (int i = 1; i < n; i++) {
int a = list.get(i);
boolean ok = false;
for (int j = i - 1; j >= 0 && !ok; j--) {
int b = list.get(j);
if (g[a][b]) {
fa[a] = b;
ok = true;
}
}
if (!ok) return 0;
}
int c = 0, ans = 1;
for (int i : set) {
int j = i;
while (fa[j] != -1) {
if (!g[i][fa[j]]) return 0;
if (cnts[i] == cnts[fa[j]]) ans = 2;
c++;
j = fa[j];
}
}
return c < m ? 0 : ans;
}
}
- 时间复杂度:令 $n$ 为
pairs的长度,统计度数和点集复杂度为 $O(n)$;最多有 $2 * n$ 个点,将点根据度数进行排序复杂度为 $O(n\log{n})$;尝试根据度数构造树的复杂度为 $O(n^2)$;检验树的合法性复杂度为 $O(n + m)$,其中 $m$ 是构造树的边数,数量级上与 $n$ 相等。整体复杂度为 $O(n^2)$ - 空间复杂度:$O(n^2)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.1719 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
