LC 686. 重复叠加字符串匹配
题目描述
这是 LeetCode 上的 686. 重复叠加字符串匹配 ,难度为 中等。
给定两个字符串 a 和 b,寻找重复叠加字符串 a 的最小次数,使得字符串 b 成为叠加后的字符串 a 的子串,如果不存在则返回 -1。
注意:字符串 "abc" 重复叠加 0 次是 "",重复叠加 1 次是 "abc",重复叠加 2 次是 "abcabc"。
示例 1:1
2
3
4
5输入:a = "abcd", b = "cdabcdab"
输出:3
解释:a 重复叠加三遍后为 "abcdabcdabcd", 此时 b 是其子串。
示例 2:1
2
3输入:a = "a", b = "aa"
输出:2
示例 3:1
2
3输入:a = "a", b = "a"
输出:1
示例 4:1
2
3输入:a = "abc", b = "wxyz"
输出:-1
提示:
- $1 <= a.length <= 10^4$
- $1 <= b.length <= 10^4$
a和b由小写英文字母组成
基本分析
首先,可以分析复制次数的「下界」和「上界」为何值:
对于「下界」的分析是容易的:至少将 a 复制长度大于等于 b 的长度,才有可能匹配。
在明确了「下界」后,再分析再经过多少次复制,能够明确得到答案,能够得到明确答案的最小复制次数即是上界。
由于主串是由 a 复制多次而来,并且是从主串中找到子串 b,因此可以明确子串的起始位置,不会超过 a 的长度。
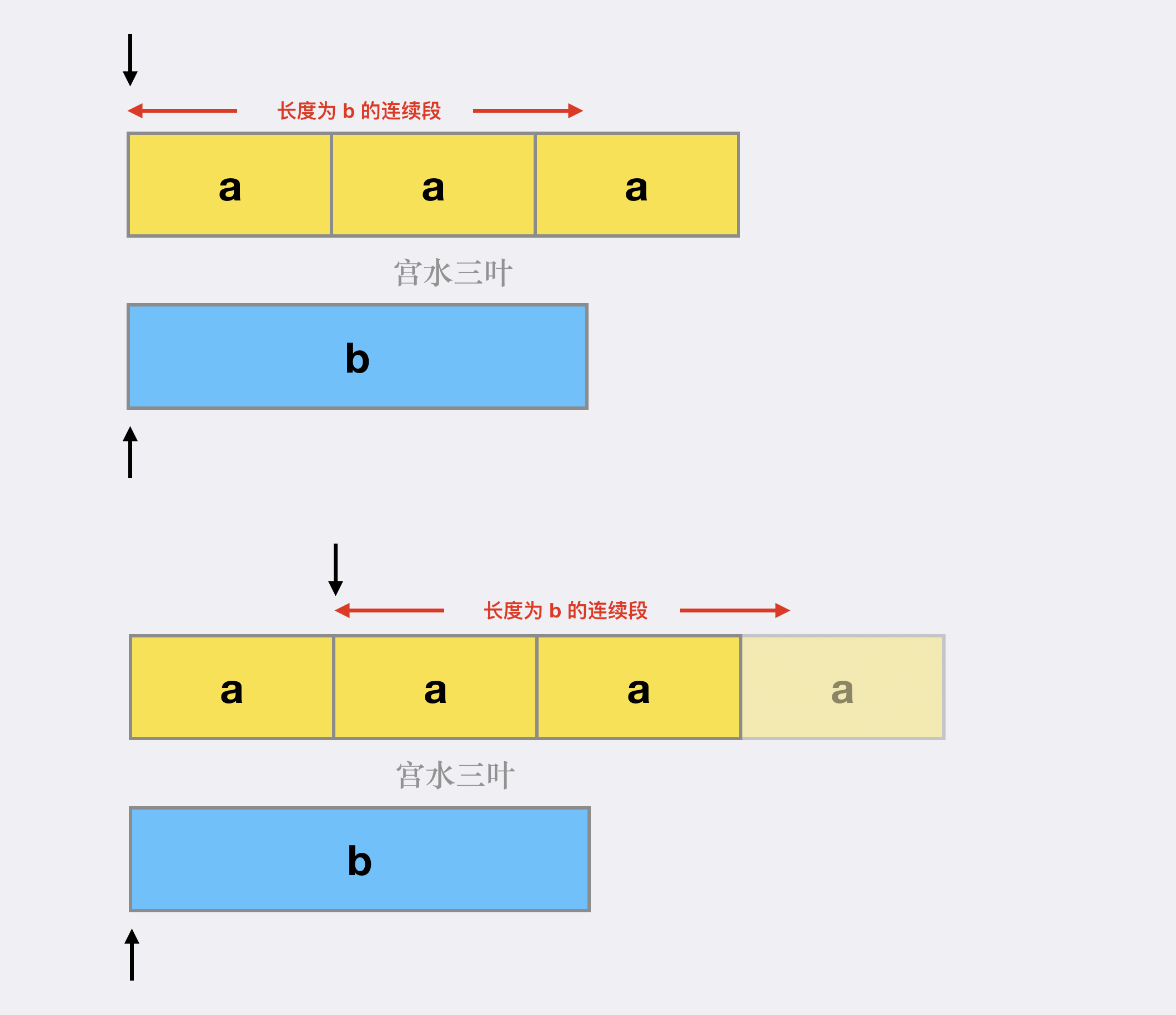
即长度越过 a 长度的起始匹配位置,必然在此前已经被匹配过了。
由此,我们可知复制次数「上界」最多为「下界 + $1$」。
令 a 的长度为 $n$,b 的长度为 $m$,下界次数为 $c1$,上界次数为 $c2 = c1 + 1$。
因此我们可以对 a 复制 $c2$ 次,得到主串后匹配 b,如果匹配成功后的结束位置不超过了 $n * c1$,说明复制 $c1$ 即可,返回 $c1$,超过则返回 $c2$;匹配不成功则返回 $-1$。
卡常
这是我最开始的 AC 版本。
虽然这是道挺显然的子串匹配问题,但是昨晚比平时晚睡了一个多小时,早上起来精神状态不是很好,身体的每个细胞都在拒绝写 KMP 🤣
就动了歪脑筋写了个「卡常」做法。
通过该做法再次印证了 LC 的评测机制十分奇葩:居然不是对每个用例单独计时,也不是算总的用例用时,而是既算单用例耗时,又算总用时??
导致我直接 TLE 了 $6$ 次才通过(从 $700$ 试到了 $100$),其中有 $4$ 次 TLE 是显示通过了所有样例,但仍然 TLE,我不理解为什么要设置这样迷惑的机制。
回到该做法本身,首先对 a 进行复制确保长度大于等于 b,然后在一定时间内,不断的「复制 - 检查」,如果在规定时间内能够找到则返回复制次数,否则返回 -1。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16import java.time.Clock;
class Solution {
public int repeatedStringMatch(String a, String b) {
StringBuilder sb = new StringBuilder();
int ans = 0;
while (sb.length() < b.length() && ++ans > 0) sb.append(a);
Clock clock = Clock.systemDefaultZone();
long start = clock.millis();
while (clock.millis() - start < 100) {
if (sb.indexOf(b) != -1) return ans;
sb.append(a);
ans++;
}
return -1;
}
}
- 时间复杂度:$O(C)$
- 空间复杂度:$O(C)$
上下界性质
通过「基本分析」后,我们发现「上下界」具有准确的大小关系,其实不需要用到「卡常」做法。
只需要进行「上界」次复制后,尝试匹配,根据匹配结果返回答案即可。
代码:1
2
3
4
5
6
7
8
9
10
11class Solution {
public int repeatedStringMatch(String a, String b) {
StringBuilder sb = new StringBuilder();
int ans = 0;
while (sb.length() < b.length() && ++ans > 0) sb.append(a);
sb.append(a);
int idx = sb.indexOf(b);
if (idx == -1) return -1;
return idx + b.length() > a.length() * ans ? ans + 1 : ans;
}
}
- 时间复杂度:需要 $\left \lceil \frac{m}{n} \right \rceil + 1$ 次拷贝 和 一次子串匹配。复杂度为 $O(n * (\left \lceil \frac{m}{n} \right \rceil + 1))$
- 空间复杂度:$O(n * (\left \lceil \frac{m}{n} \right \rceil + 1))$
KMP
其中 indexOf 部分可以通过 KMP/字符串哈希 实现,不熟悉 KMP 的同学,可以查看 一文详解 KMP 算法,里面通过大量配图讲解了 KMP 的匹配过程与提供了实用模板。
使用 KMP 代替 indexOf 可以有效利用主串是由多个 a 复制而来的性质。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47class Solution {
public int repeatedStringMatch(String a, String b) {
StringBuilder sb = new StringBuilder();
int ans = 0;
while (sb.length() < b.length() && ++ans > 0) sb.append(a);
sb.append(a);
int idx = strStr(sb.toString(), b);
if (idx == -1) return -1;
return idx + b.length() > a.length() * ans ? ans + 1 : ans;
}
int strStr(String ss, String pp) {
if (pp.isEmpty()) return 0;
// 分别读取原串和匹配串的长度
int n = ss.length(), m = pp.length();
// 原串和匹配串前面都加空格,使其下标从 1 开始
ss = " " + ss;
pp = " " + pp;
char[] s = ss.toCharArray();
char[] p = pp.toCharArray();
// 构建 next 数组,数组长度为匹配串的长度(next 数组是和匹配串相关的)
int[] next = new int[m + 1];
// 构造过程 i = 2,j = 0 开始,i 小于等于匹配串长度 【构造 i 从 2 开始】
for (int i = 2, j = 0; i <= m; i++) {
// 匹配不成功的话,j = next(j)
while (j > 0 && p[i] != p[j + 1]) j = next[j];
// 匹配成功的话,先让 j++
if (p[i] == p[j + 1]) j++;
// 更新 next[i],结束本次循环,i++
next[i] = j;
}
// 匹配过程,i = 1,j = 0 开始,i 小于等于原串长度 【匹配 i 从 1 开始】
for (int i = 1, j = 0; i <= n; i++) {
// 匹配不成功 j = next(j)
while (j > 0 && s[i] != p[j + 1]) j = next[j];
// 匹配成功的话,先让 j++,结束本次循环后 i++
if (s[i] == p[j + 1]) j++;
// 整一段匹配成功,直接返回下标
if (j == m) return i - m;
}
return -1;
}
}
- 时间复杂度:需要 $\left \lceil \frac{m}{n} \right \rceil + 1$ 次拷贝 和 一次子串匹配。复杂度为 $O(n * (\left \lceil \frac{m}{n} \right \rceil + 1))$
- 空间复杂度:$O(n * (\left \lceil \frac{m}{n} \right \rceil + 1))$
字符串哈希
结合「基本分析」,我们知道这本质是一个子串匹配问题,我们可以使用「字符串哈希」来解决。
令 a 的长度为 $n$,b 的长度为 $m$。
仍然是先将 a 复制「上界」次,得到主串 ss,目的是从 ss 中检测是否存在子串为 b。
在字符串哈希中,为了方便,我们将 ss 和 b 进行拼接,设拼接后长度为 $len$,那么 b 串的哈希值为 $[len - m + 1, len]$ 部分(下标从 $1$ 开始),记为 $target$。
然后在 $[1, n]$ 范围内枚举起点,尝试找长度为 $m$ 的哈希值与 $target$ 相同的哈希值。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public int repeatedStringMatch(String a, String b) {
StringBuilder sb = new StringBuilder();
int ans = 0;
while (sb.length() < b.length() && ++ans > 0) sb.append(a);
sb.append(a);
int idx = strHash(sb.toString(), b);
if (idx == -1) return -1;
return idx + b.length() > a.length() * ans ? ans + 1 : ans;
}
int strHash(String ss, String b) {
int P = 131;
int n = ss.length(), m = b.length();
String str = ss + b;
int len = str.length();
int[] h = new int[len + 10], p = new int[len + 10];
h[0] = 0; p[0] = 1;
for (int i = 0; i < len; i++) {
p[i + 1] = p[i] * P;
h[i + 1] = h[i] * P + str.charAt(i);
}
int r = len, l = r - m + 1;
int target = h[r] - h[l - 1] * p[r - l + 1]; // b 的哈希值
for (int i = 1; i <= n; i++) {
int j = i + m - 1;
int cur = h[j] - h[i - 1] * p[j - i + 1]; // 子串哈希值
if (cur == target) return i - 1;
}
return -1;
}
}
- 时间复杂度:需要 $\left \lceil \frac{m}{n} \right \rceil + 1$ 次拷贝 和 一次子串匹配。复杂度为 $O(n * (\left \lceil \frac{m}{n} \right \rceil + 1))$
- 空间复杂度:$O(n * (\left \lceil \frac{m}{n} \right \rceil + 1))$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.686 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
