LC 375. 猜数字大小 II
题目描述
这是 LeetCode 上的 375. 猜数字大小 II ,难度为 中等。
我们正在玩一个猜数游戏,游戏规则如下:
- 我从
1到n之间选择一个数字。 - 你来猜我选了哪个数字。
- 如果你猜到正确的数字,就会 赢得游戏 。
- 如果你猜错了,那么我会告诉你,我选的数字比你的 更大或者更小 ,并且你需要继续猜数。
- 每当你猜了数字
x并且猜错了的时候,你需要支付金额为x的现金。如果你花光了钱,就会 输掉游戏 。
给你一个特定的数字 n ,返回能够 确保你获胜 的最小现金数,不管我选择那个数字 。
示例 1: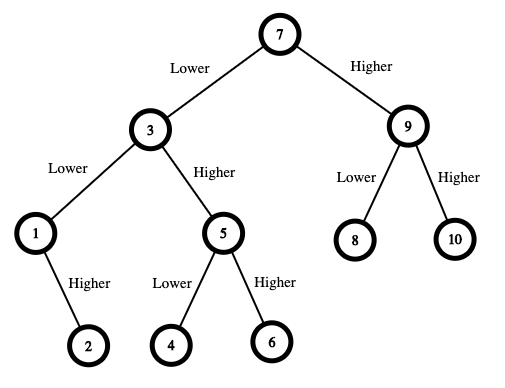
1 | |
示例 2:1
2
3
4
5输入:n = 1
输出:0
解释:只有一个可能的数字,所以你可以直接猜 1 并赢得游戏,无需支付任何费用。
示例 3:1
2
3
4
5
6
7
8
9输入:n = 2
输出:1
解释:有两个可能的数字 1 和 2 。
- 你可以先猜 1 。
- 如果这是我选中的数字,你的总费用为 $0 。否则,你需要支付 $1 。
- 如果我的数字更大,那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏,总费用为 $1 。
最糟糕的情况下,你需要支付 $1 。
提示:
- 1 <= n <= 200
基本分析
这不是一道可通过「二分」求解的题目,主要原因为每次惩罚的金额不固定,最小惩罚次数不等同于猜中数字的最小成本。
记忆化搜索
比较容易想到的做法为使用「递归」进行求解。
设计递归函数为 int dfs(int l, int r) 传入参数 l 和 r 代表在范围 $[l, r]$ 内进行猜数,返回值为在 $[l, r]$ 内猜中数字至少需要多少钱。
我们可决策的部分为「选择猜哪个数 $x$」,而不可决策的是「选择某个数 $x$ 之后(假设没有猜中),真实值会落在哪边」。
因此为求得「最坏情况下最好」的结果,我们应当取所有的 $x$ 中的最小值。
最后,为减少重复计算,我们需要在「递归」基础上加入记忆化搜索。并且当我们使用 static 修饰 $cache$ 时,可以确保每个区间的计算在所有样例中只会发生一次。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
static int N = 210;
static int[][] cache = new int[N][N];
public int getMoneyAmount(int n) {
return dfs(1, n);
}
int dfs(int l, int r) {
if (l >= r) return 0;
if (cache[l][r] != 0) return cache[l][r];
int ans = 0x3f3f3f3f;
for (int x = l; x <= r; x++) {
// 当选择的数位 x 时,至少需要 cur 才能猜中数字
int cur = Math.max(dfs(l, x - 1), dfs(x + 1, r)) + x;
// 在所有我们可以决策的数值之间取最优
ans = Math.min(ans, cur);
}
cache[l][r] = ans;
return ans;
}
}
- 时间复杂度:$O(n^3)$
- 空间复杂度:忽略递归带来的额外空间开销,复杂度为 $O(n^2)$
区间 DP
同样能够通过「递推」来进行求解。
通过「记忆化搜索」的递归过程,我们发现,在求解 $[l, r]$ 的最小成本时,需要依赖于 $[l, i - 1]$ 和 $[i + 1, r]$ 这样的比 $[l, r]$ 更小的区间。
这引导我们使用「区间 DP」进行求解,对「区间 DP」不了解的同学可以先看 「区间 DP」入门题 。
定义 $f[l][r]$ 为考虑在 $[l, r]$ 范围内进行猜数的最小成本。
不失一般性的考虑 $f[l][r]$ 该如何计算。同样的,我们可决策的部分为「选择猜哪个数 $x$」,而不可决策的是「选择某个数 $x$ 之后(假设没有猜中),真实值在落在哪边」。
我们对本次选择哪个数进行讨论,假设本次选择的数值为 $x$ ( $l <= x <= r$ ),则有 $cur = \max(f[l][x - 1], f[x + 1][r]) + x$
最终的 $f[l][r]$ 为所有可选的数值 $x$ 中的最小值。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public int getMoneyAmount(int n) {
int[][] f = new int[n + 10][n + 10];
for (int len = 2; len <= n; len++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
f[l][r] = 0x3f3f3f3f;
for (int x = l; x <= r; x++) {
int cur = Math.max(f[l][x - 1], f[x + 1][r]) + x;
f[l][r] = Math.min(f[l][r], cur);
}
}
}
return f[1][n];
}
}
- 时间复杂度:$O(n^3)$
- 空间复杂度:$O(n^2)$
打表
由于任意的 $[l,r]$ 对应结果均为定值,可以进行打表预处理。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
static int N = 200;
static int[][] f = new int[N + 10][N + 10];
static {
for (int len = 2; len <= N; len++) {
for (int l = 1; l + len - 1 <= N; l++) {
int r = l + len - 1;
f[l][r] = 0x3f3f3f3f;
for (int x = l; x <= r; x++) {
int cur = Math.max(f[l][x - 1], f[x + 1][r]) + x;
f[l][r] = Math.min(f[l][r], cur);
}
}
}
}
public int getMoneyAmount(int n) {
return f[1][n];
}
}
- 时间复杂度:$O(C^3)$
- 空间复杂度:$O(C^2)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.375 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
