LC 2477. 到达首都的最少油耗
题目描述
这是 LeetCode 上的 2477. 到达首都的最少油耗 ,难度为 中等。
给你一棵 n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 到 n - 1,且恰好有 n - 1 条路。
0 是首都。给你一个二维整数数组 roads,其中 $roads[i] = [a{i}, b{i}]$ ,表示城市 $a{i}$ 和 $b{i}$ 之间有一条双向路。
每个城市里有一个代表,他们都要去首都参加一个会议。
每座城市里有一辆车,给你一个整数 seats 表示每辆车里面座位的数目。
城市里的代表可以选择乘坐所在城市的车,或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。
请你返回到达首都最少需要多少升汽油。
示例 1:
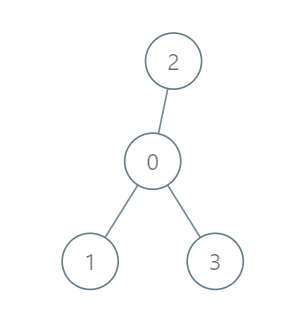
1 | |
示例 2:
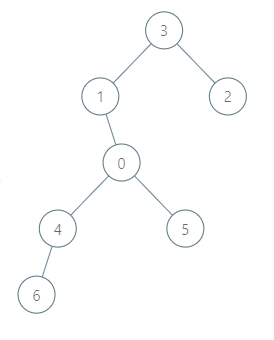
1 | |
示例 3:

1 | |
提示:
- $1 <= n <= 105$
- $roads.length = n - 1$
- $roads[i].length = 2$
- $0 <= a{i}, b{i} < n$
- $a{i} != b{i}$
roads表示一棵合法的树。- $1 <= seats <= 10^5$
DFS
将双向图看作是以节点 0 为根的有向树,从每个节点出发往 0 前行,可看作是自底向上的移动过程。
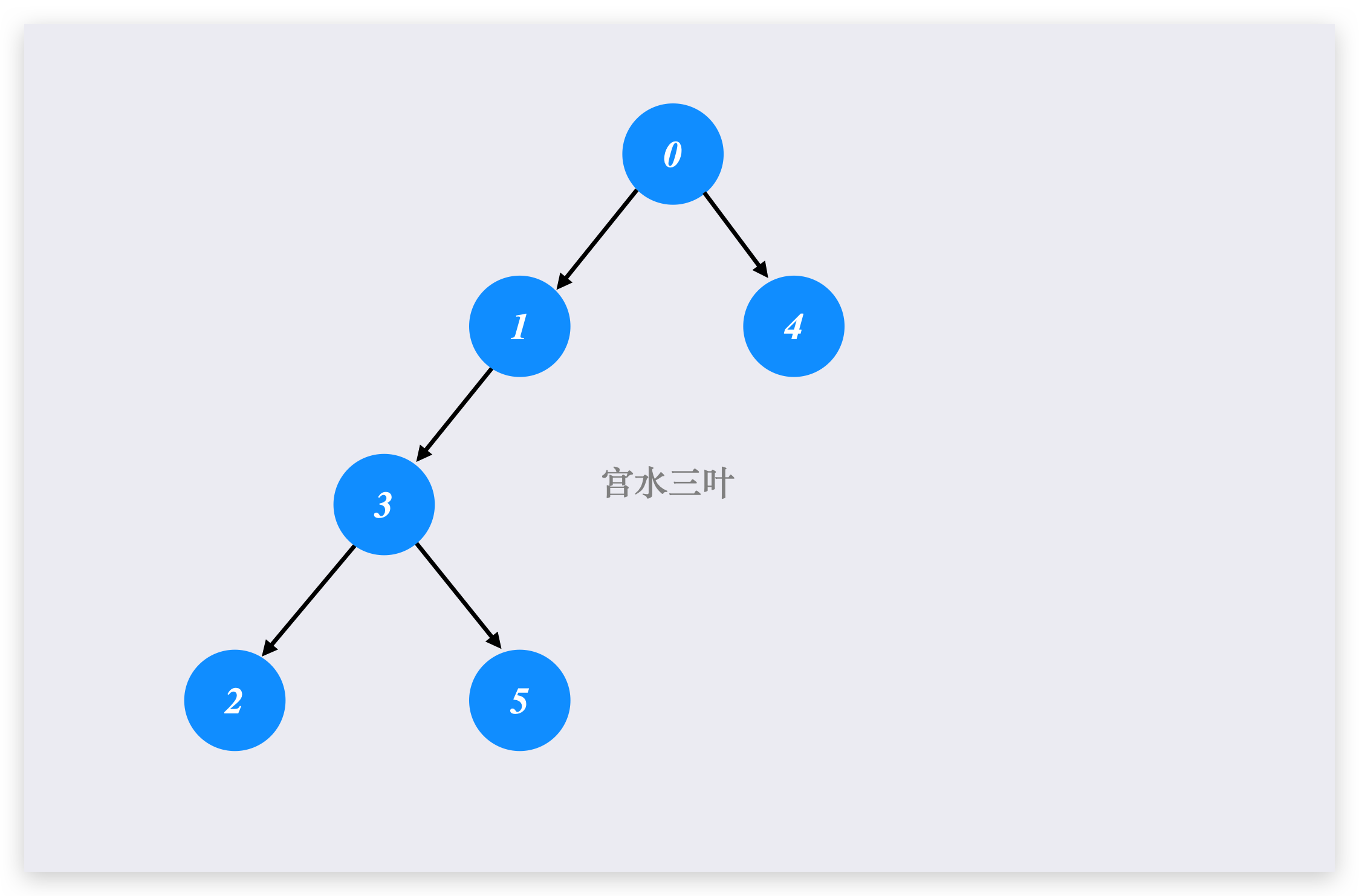
当 seats = 1 时,每个节点前往 0 的过程相互独立,总油耗为每节点到 0 的最短距离之和。
当 seats 不为 1 时,考虑组成顺风车,此时总的油耗不该超过 seats = 1 的情况。
不难发现,只有「深度大的节点,在前往 0 过程中,搭乘深度小顺风车」可减少油耗(例如在上图节点 3 在经过节点 1 时搭乘顺风车,可与节点 1 合计使用一份油耗前往到 0),否则如果是深度小的节点先往深度大的节点走,再一同前往 0,会额外多经过某些边,产生不必要的油耗。
考虑组成顺风车时,总油耗该如何计算。
基于上述分析,无论 seats 是否为 $1$(是否组成顺风车),每个节点前往 0 的路径总是不变,即经过的边固定不变,必然是自底向上。
因此我们可统计每条边会被多少个节点经过,通过 DFS 统计「以每个节点为根时,子树的节点数量」即是经过该节点往上的边。
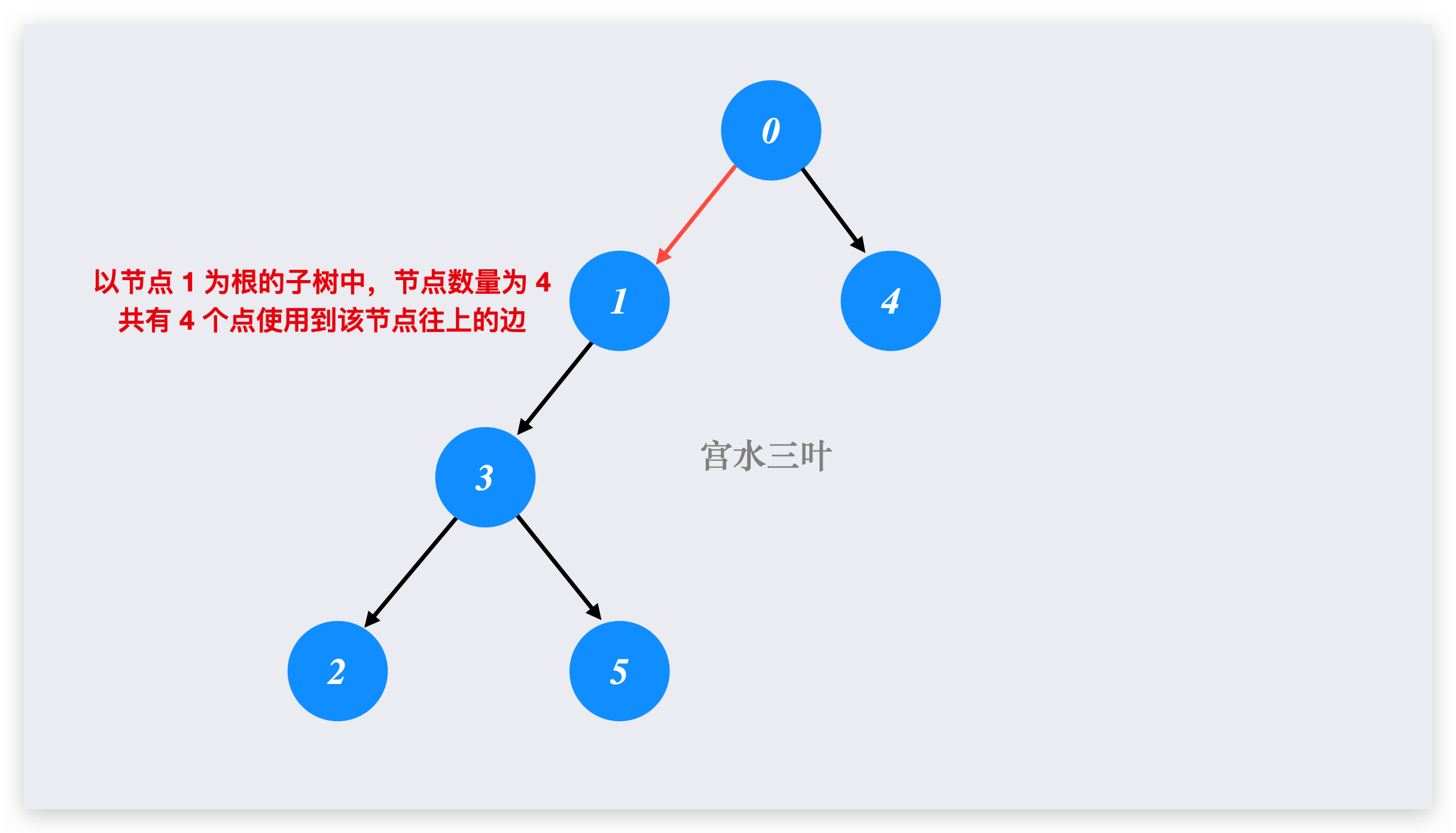
知道经过某条边的节点数量 cnt 后,$\left \lceil \frac{cnt}{seats} \right \rceil$ 即是该边对答案的贡献。
Java 代码:
1 | |
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
int N = 100010, M = 2 * N, idx = 0;
int he[100010], e[200020], ne[200020];
long long ans = 0;
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
int n = roads.size() + 1;
memset(he, -1, sizeof(he));
for (auto& r : roads) {
int a = r[0], b = r[1];
add(a, b); add(b, a);
}
dfs(0, -1, seats);
return ans;
}
int dfs(int u, int fa, int t) {
int cnt = 1;
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
cnt += dfs(j, u, t);
}
if (u != 0) ans += ceil(cnt * 1.0 / t);
return cnt;
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution:
def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
n, m, ans = len(roads) + 1, len(roads) * 2 + 1, 0
he, e, ne, idx = [-1] * n, [0] * m, [0] * m, 0
def add(a, b):
nonlocal idx
e[idx] = b
ne[idx] = he[a]
he[a] = idx
idx += 1
def dfs(u, fa, t):
nonlocal ans
cnt = 1
i = he[u]
while i != -1:
j, i = e[i], ne[i]
if j == fa: continue
cnt += dfs(j, u, t)
if u != 0:
ans += math.ceil(cnt * 1.0 / t)
return cnt
for a, b in roads:
add(a, b)
add(b, a)
dfs(0, -1, seats)
return ans
TypeScript 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25function minimumFuelCost(roads: number[][], seats: number): number {
const n = roads.length + 1, m = n * 2;
const he = Array(n).fill(-1), e = Array(m).fill(0), ne = Array(m).fill(0);
let ans = 0, idx = 0;
const add = function(a: number, b: number) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
const dfs = function(u: number, fa: number, t: number): number {
let cnt = 1;
for (let i = he[u]; i != -1; i = ne[i]) {
const j = e[i];
if (j == fa) continue;
cnt += dfs(j, u, t);
}
if (u != 0) ans += Math.ceil(cnt * 1.0 / t);
return cnt;
}
for (const [a, b] of roads) {
add(a, b); add(b, a);
}
dfs(0, -1, seats);
return ans;
};
- 时间复杂度:建图复杂度为 $O(n)$;递归统计每个子树节点数量并计算油耗复杂度 $O(n)$;整体复杂度为 $O(n)$
- 空间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.2477 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
