LC 1334. 阈值距离内邻居最少的城市
题目描述
这是 LeetCode 上的 1334. 阈值距离内邻居最少的城市 ,难度为 中等。
有 $n$ 个城市,按从 $0$ 到 $n-1$ 编号。
给你一个边数组 edges,其中 $edges[i] = [from{i}, to{i}, weight{i}]$ 代表 $from{i}$ 和 $to_{i}$ 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少,且路径距离最大为 distanceThreshold 的城市。
如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 $i$ 和 $j$ 的路径的距离等于沿该路径的所有边的权重之和。
示例 1:
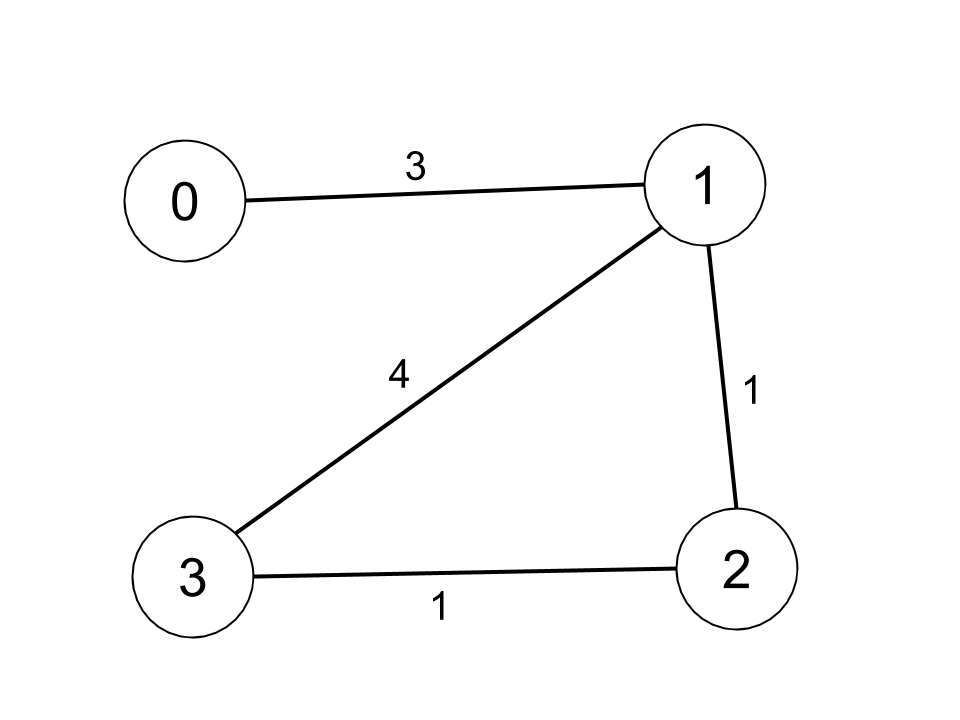
1 | |
示例 2:
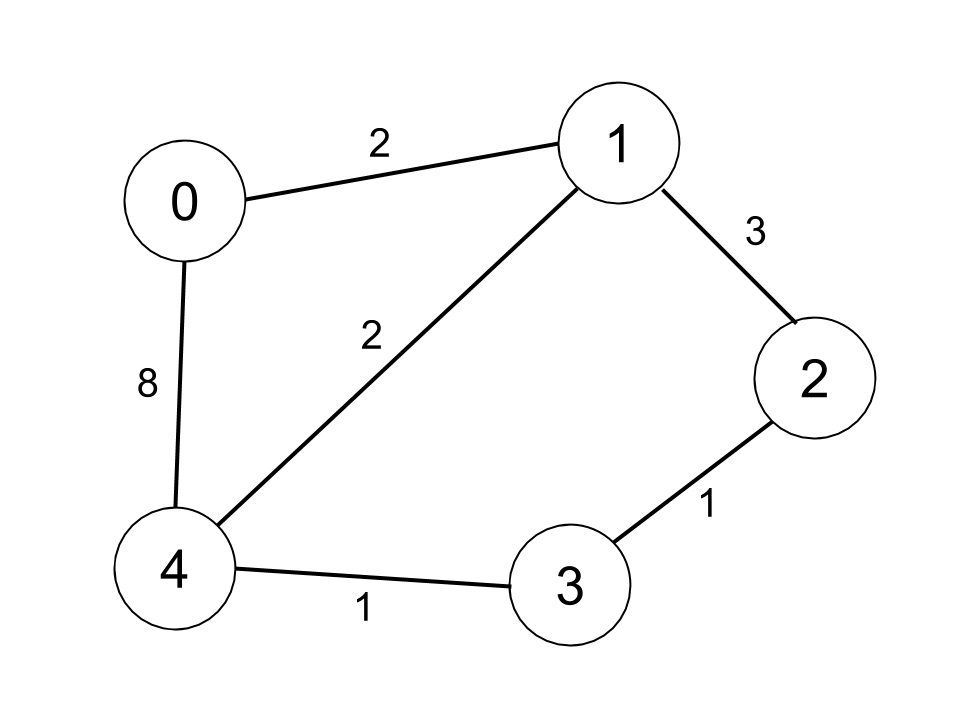
1 | |
提示:
- $2 <= n <= 100$
- $1 <= edges.length <= \frac{n \times (n - 1)}{2}$
- $edges[i].length = 3$
- $0 <= from{i} < to{i} < n$
- $1 <= weight_{i}, distanceThreshold <= 10^4$
- 所有 $(from{i}, to{i})$ 都是不同的。
基本分析
若能预处理图中任意两点 $i$ 和 $j$ 的最短距离 dist,那么统计每个点 $i$ 在图中有多少满足 $dist[j] \leq distanceThreshold$ 的点 $j$ 即为答案。
于是问题转换为:如何求解给定图中,任意两点的最短距离。
存图
在学习最短路之前,我们先搞懂众多图论问题的前置 🧀 :存图。
为了方便,我们约定 $n$ 为点数,$m$ 为边数。
根据点和边的数量级关系,可以将图分成如下两类:
- 稠密图:边数较多,边数接近于点数的平方,即 $m \approx n^2$
- 稀疏图:边数较少,边数接近于点数,即 $m \approx n$
同时,根据「稠密图」还是「稀疏图」,我们有如下几种存图方式:
1. 邻接矩阵(稠密图)
这是一种使用二维矩阵来进行存图的方式。
1 | |
2. 邻接表(稀疏图)
邻接表又叫链式前向星,是另一种常见的存图方式,实现代码与「使用数组存储单链表」一致(头插法)。
1 | |
首先 idx 是用来对边进行编号的,然后对存图用到的几个数组作简单解释:
he数组:存储是某个节点所对应的边的集合(链表)的头结点;e数组:由于访问某一条边指向的节点;ne数组:由于是以链表的形式进行存边,该数组就是用于找到下一条边;w数组:用于记录某条边的权重为多少。
当我们想要遍历所有由 a 点发出的边时,可以使用如下方式:
1 | |
3. 类
这是最简单,但使用频率最低的存图方式。
只有当我们需要确保某个操作复杂度为严格 $O(m)$ 时,才会考虑使用。
具体的,建立一个类来记录有向边信息:
1 | |
随后,使用诸如 List 的容器,存起所有边对象。在需要遍历所有边时,对容器进行进行遍历:
1 | |
综上,第 $3$ 种方式,往往是 OJ 给我们边信息的方式,我们自己几乎不会用这种方式建图。
实际运用中,熟练掌握「如何根据点和边的数量级关系,来决定使用邻接矩阵(稠密图)还是邻接表(稀疏图)」即可。
Floyd(邻接矩阵)
Floyd 算法作为「多源汇最短路」算法,对于本题尤其适合。
Floyd 算法基于「动态规划」,其原始三维状态定义为 $dist[p][i][j]$,表示「所有从点 $i$ 到点 $j$,且允许经过点集 $(1, … , p)$ 的路径」中的最短距离。
状态转移方程:
$dist[p - 1][i][j]$ 代表从 $i$ 到 $j$ 但必然不经过点 $p$ 的路径,$dist[p - 1][i][p] + dist[p - 1][p][j]$ 代表必然经过点 $p$ 的路径,两者中取较小值更新 $dist[p][i][j]$。
不难发现任意的 $dist[p][X][Y]$ 依赖于 $dist[p - 1][X][Y]$,可采用「滚动数组」的方式进行优化。
将 dist 声明为二维数组,$dist[i][j]$ 代表从点 $i$ 到点 $j$ 的最短距离,并采取 [枚举中转点 - 枚举起点 - 枚举终点] 三层循环的方式更新 $dist[i][j]$。
如此一来,跑一遍 Floyd 算法便可得出任意两点的最短距离。
通过上述推导,不难发现,我们并没提及边权的正负问题,因此 Floyd 算法对边权的正负没有限制要求(可处理正负权边的图),且能利用 Floyd 算法可能够对图中负环进行判定。
Java 代码:
1 | |
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
vector<vector<int>> g(n, vector<int>(n, 0x3f3f3f3f));
// 初始化邻接矩阵
for (int i = 0; i < n; i++) g[i][i] = 0;
// 存图
for (const auto& e : edges) {
int a = e[0], b = e[1], c = e[2];
g[a][b] = g[b][a] = min(g[a][b], c);
}
// 最短路
floyd(g);
// 统计答案
int ans = -1, cnt = n + 10;
for (int i = 0; i < n; i++) {
int cur = 0;
for (int j = 0; j < n; j++) {
if (i != j && g[i][j] <= distanceThreshold) cur++;
}
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
}
void floyd(vector<vector<int>>& g) {
int n = g.size();
// floyd 基本流程为三层循环: [枚举中转点 - 枚举起点 - 枚举终点] => 松弛操作
for (int p = 0; p < n; p++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
g[i][j] = min(g[i][j], g[i][p] + g[p][j]);
}
}
}
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
def floyd(g: List[List[int]]) -> None:
n = len(g)
# floyd 基本流程为三层循环: [枚举中转点 - 枚举起点 - 枚举终点] => 松弛操作
for p in range(n):
for i in range(n):
for j in range(n):
g[i][j] = min(g[i][j], g[i][p] + g[p][j])
g = [[float('inf')] * n for _ in range(n)]
# 初始化邻接矩阵
for i in range(n):
g[i][i] = 0
# 存图
for a, b, c in edges:
g[a][b] = g[b][a] = min(g[a][b], c)
# 最短路
floyd(g)
# 统计答案
ans, cnt = -1, n + 10
for i in range(n):
cur = sum(1 for j in range(n) if i != j and g[i][j] <= distanceThreshold)
if cur <= cnt:
cnt, ans = cur, i
return ans
TypeScript 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33function findTheCity(n: number, edges: number[][], distanceThreshold: number): number {
const floyd = function (g: number[][]): void {
const n = g.length;
// floyd 基本流程为三层循环: [枚举中转点 - 枚举起点 - 枚举终点] => 松弛操作
for (let p = 0; p < n; p++) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
g[i][j] = Math.min(g[i][j], g[i][p] + g[p][j]);
}
}
}
}
const g = Array.from({ length: n }, () => Array(n).fill(0x3f3f3f3f));
// 初始化邻接矩阵
for (let i = 0; i < n; i++) g[i][i] = 0;
// 存图
for (const [a, b, c] of edges) g[a][b] = g[b][a] = Math.min(g[a][b], c);
// 最短路
floyd(g);
// 统计答案
let ans = -1, cnt = n + 10;
for (let i = 0; i < n; i++) {
let cur = 0;
for (let j = 0; j < n; j++) {
if (i !== j && g[i][j] <= distanceThreshold) cur++;
}
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
};
- 时间复杂度:初始化邻接矩阵和建图复杂度为 $O(n^2 + m)$;
floyd算法复杂度为 $O(n^3)$;统计答案复杂度为 $O(n^2)$;整体复杂度为 $O(n^3 + m)$ - 空间复杂度:$O(n^2)$
朴素 Dijkstra(邻接矩阵)
最为经典的「单源最短路」算法,通常搭配「邻接矩阵」使用,应用在边数较多的“稠密图”上。
朴素 Dijkstra 算法基于「贪心」,通过维护一维的距离数组 dist 实现,$dist[i]$ 表示从源点出发到点 $i$ 的最短距离。
朴素 Dijkstra 算法在每一次迭代中,都选择 dist 中值最小的点进行松弛操作,逐渐扩展最短路径范围。
Java 代码:
1 | |
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution {
public:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
vector<vector<int>> g(n, vector<int>(n, 0x3f3f3f3f));
// 初始化邻接矩阵
for (int i = 0; i < n; i++) g[i][i] = 0;
// 存图
for (const auto& e : edges) {
int a = e[0], b = e[1], c = e[2];
g[a][b] = g[b][a] = min(g[a][b], c);
}
int ans = -1, cnt = n + 10;
for (int i = 0; i < n; i++) {
// 单源最短路
vector<int> dist = dijkstra(g, i);
int cur = count_if(dist.begin(), dist.end(), [distanceThreshold](int d) { return d <= distanceThreshold; });
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
}
vector<int> dijkstra(const vector<vector<int>>& g, int x) {
int n = g.size();
vector<bool> vis(n, false);
vector<int> dist(n, 0x3f3f3f3f);
// 只有起点最短距离为 0
dist[x] = 0;
// 有多少个点就迭代多少次
for (int k = 0; k < n; k++) {
// 每次找到「最短距离最小」且「未被更新」的点 t
int t = -1;
for (int i = 0; i < n; i++) {
if (!vis[i] && (t == -1 || dist[i] < dist[t])) t = i;
}
// 标记点 t 为已更新
vis[t] = true;
// 用点 t 的「最小距离」更新其他点
for (int i = 0; i < n; i++) dist[i] = min(dist[i], dist[t] + g[t][i]);
}
return dist;
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
def dijkstra(g, x):
n = len(g)
vis = [False] * n
dist = [float('inf')] * n
# 只有起点最短距离为 0
dist[x] = 0
# 有多少个点就迭代多少次
for k in range(n):
# 每次找到「最短距离最小」且「未被更新」的点 t
t = min((i for i in range(n) if not vis[i]), key=lambda i: dist[i])
# 标记点 t 为已更新
vis[t] = True
# 用点 t 的「最小距离」更新其他点
for i in range(n):
dist[i] = min(dist[i], dist[t] + g[t][i])
return dist
g = [[float('inf')] * n for _ in range(n)]
# 初始化邻接矩阵
for i in range(n):
g[i][i] = 0
# 存图
for a, b, c in edges:
g[a][b] = g[b][a] = min(g[a][b], c)
ans, cnt = -1, n + 10
for i in range(n):
# 单源最短路
dist = dijkstra(g, i)
cur = sum(1 for j in range(n) if i != j and dist[j] <= distanceThreshold)
if cur <= cnt:
cnt, ans = cur, i
return ans
TypeScript 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37function findTheCity(n: number, edges: number[][], distanceThreshold: number): number {
const dijkstra = function (g: number[][], x: number): number[] {
const n = g.length;
const vis = Array(n).fill(false), dist = Array(n).fill(0x3f3f3f3f);
// 只有起点最短距离为 0
dist[x] = 0;
// 有多少个点就迭代多少次
for (let k = 0; k < n; k++) {
// 每次找到「最短距离最小」且「未被更新」的点 t
let t = -1;
for (let i = 0; i < n; i++) {
if (!vis[i] && (t === -1 || dist[i] < dist[t])) t = i;
}
// 标记点 t 为已更新
vis[t] = true;
// 用点 t 的「最小距离」更新其他点
for (let i = 0; i < n; i++) dist[i] = Math.min(dist[i], dist[t] + g[t][i]);
}
return dist;
}
const g = Array.from({ length: n }, () => Array(n).fill(0x3f3f3f3f));
// 初始化邻接矩阵
for (let i = 0; i < n; i++) g[i][i] = 0;
// 存图
for (const [a, b, c] of edges) g[a][b] = g[b][a] = Math.min(g[a][b], c);
let ans = -1, cnt = n + 10;
for (let i = 0; i < n; i++) {
// 单源最短路
const dist = dijkstra(g, i);
const cur = dist.filter(d => d <= distanceThreshold).length;
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
};
- 时间复杂度:初始化邻接矩阵和建图复杂度为 $O(n^2 + m)$;统计答案时,共执行 $n$ 次朴素
dijkstra算法,朴素dijkstra复杂度为 $O(n^2)$,总复杂度为 $O(n^3)$。整体复杂度为 $O(n^3 + m)$ - 空间复杂度:$O(n^2)$
堆优化 Dijkstra(邻接表)
堆优化 Dijkstra 算法与朴素 Dijkstra 算法都是「单源最短路」算法。
堆优化 Dijkstra 算法通过数据结构「优先队列(堆)」来优化朴素 Dijkstra 中的“找 dist 中值最小的点”的过程。
相比于复杂度与边数无关的 $O(n^2)$ 朴素 Dijkstra 算法,复杂度与边数相关的 $O(m\log{n})$ 堆优化 Dijkstra 算法更适合边较少的“稀疏图”。
Java 代码:
1 | |
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58class Solution {
public:
static const int N = 110, M = N * N;
int he[N], e[M], ne[M], w[M], idx, n, INF = 0x3f3f3f3f;
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
w[idx] = c;
he[a] = idx++;
}
int findTheCity(int _n, vector<vector<int>>& edges, int distanceThreshold) {
n = _n;
// 初始化链表头
fill(he, he + n, -1);
// 存图
for (const auto& e : edges) {
int a = e[0], b = e[1], c = e[2];
add(a, b, c); add(b, a, c);
}
// 统计答案
int ans = -1, cnt = n + 10;
for (int i = 0; i < n; i++) {
// 单源最短路
vector<int> dist = dijkstra(i);
int cur = count_if(dist.begin(), dist.end(), [distanceThreshold](int d) { return d <= distanceThreshold; });
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
}
vector<int> dijkstra(int x) {
// 起始先将所有的点标记为「未更新」和「距离为正无穷」
vector<int> dist(n, INF);
vector<bool> vis(n, false);
dist[x] = 0;
// 使用「优先队列」存储所有可用于更新的点
// 以 (到起点的距离, 点编号) 进行存储,优先弹出「最短距离」较小的点
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
q.push({0, x});
while (!q.empty()) {
// 每次从「优先队列」中弹出
auto [step, u] = q.top();
q.pop();
// 如果弹出的点被标记「已更新」,则跳过
if (vis[u]) continue;
// 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[u] = true;
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] <= dist[u] + w[i]) continue;
dist[j] = dist[u] + w[i];
q.push({dist[j], j});
}
}
return dist;
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55import heapq
class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
N, M, INF, idx = 110, 110 * 110, float('inf'), 0
he, e, ne, w = [-1] * N, [0] * M, [0] * M, [0] * M
def add(a, b, c):
nonlocal idx
e[idx] = b
ne[idx] = he[a]
w[idx] = c
he[a] = idx
idx += 1
def dijkstra(x):
# 起始先将所有的点标记为「未更新」和「距离为正无穷」
dist = [float('inf')] * n
vis = [False] * n
dist[x] = 0
# 使用「优先队列」存储所有可用于更新的点
# 以 (点编号, 到起点的距离) 进行存储,优先弹出「最短距离」较小的点
q = [(0, x)]
heapq.heapify(q)
while q:
# 每次从「优先队列」中弹出
step, u = heapq.heappop(q)
# 如果弹出的点被标记「已更新」,则跳过
if vis[u]: continue
# 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[u] = True
i = he[u]
while i != -1:
j, c = e[i], w[i]
i = ne[i]
if dist[j] <= dist[u] + c: continue
dist[j] = dist[u] + c
heapq.heappush(q, (dist[j], j))
return dist
# 初始化链表头
he = [-1] * N
# 存图
for a, b, c in edges:
add(a, b, c)
add(b, a, c)
# 统计答案
ans, cnt = -1, n + 10
for i in range(n):
# 单源最短路
dist = dijkstra(i)
cur = sum(1 for j in range(n) if i != j and dist[j] <= distanceThreshold)
if cur <= cnt:
cnt, ans = cur, i
return ans
- 时间复杂度:初始化邻接表和建图复杂度为 $O(n + m)$;统计答案时,共执行 $n$ 次堆优化
dijkstra算法,堆优化dijkstra复杂度为 $O(m\log{n})$,总复杂度为 $O(nm\log{n})$。整体复杂度为 $O(nm\log{n})$ - 空间复杂度:$O(n + m)$
Bellman Ford(类)
虽然题目规定了不存在「负权边」,但我们仍然可以使用可以在「负权图中求最短路」的 Bellman Ford 进行求解,该算法也是「单源最短路」算法,复杂度为 $O(n \times m)$。
通常为了确保 $O(n \times m)$,可以单独建一个类代表边,将所有边存入集合中,在 $n$ 次松弛操作中直接对边集合进行遍历。
由于本题边数量级为 $n^2$,共对 $n$ 个点执行 Bellman Ford 算法,因此整体会去到 $O(n^4)$,有 TLE 风险。
Java 代码:
1 | |
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
public:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
int ans = -1, cnt = n + 10;
for (int i = 0; i < n; i++) {
vector<int> dist = bf(edges, i, n);
int cur = 0;
for (int j = 0; j < n; j++) {
if (i != j && dist[j] <= distanceThreshold) cur++;
}
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
}
vector<int> bf(vector<vector<int>>& edges, int x, int n) {
// 起始先将所有的点标记为「距离为正无穷」, 只有起点最短距离为 0
vector<int> dist(n, 0x3f3f3f3f);
dist[x] = 0;
// 有多少个点就迭代多少次
for (int k = 0; k < n; k++) {
// 每次都使用上一次迭代的结果,执行松弛操作
vector<int> prev = dist;
for (const auto& e : edges) {
int a = e[0], b = e[1], c = e[2];
dist[b] = min(dist[b], prev[a] + c);
dist[a] = min(dist[a], prev[b] + c);
}
}
return dist;
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
def bf(edges: List[List[int]], x: int, n: int) -> List[int]:
# 起始先将所有的点标记为「距离为正无穷」, 只有起点最短距离为 0
dist = [float('inf')] * n
dist[x] = 0
# 有多少个点就迭代多少次
for k in range(n):
# 每次都使用上一次迭代的结果,执行松弛操作
prev = dist.copy()
for a, b, c in edges:
dist[b] = min(dist[b], prev[a] + c)
dist[a] = min(dist[a], prev[b] + c)
return dist
ans, cnt = -1, n + 10
for i in range(n):
dist = bf(edges, i, n)
cur = sum(1 for j in range(n) if i != j and dist[j] <= distanceThreshold)
if cur <= cnt:
cnt, ans = cur, i
return ans
TypeScript 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31function findTheCity(n: number, edges: number[][], distanceThreshold: number): number {
const bf = function(x: number): number[] {
// 起始先将所有的点标记为「距离为正无穷」, 只有起点最短距离为 0
const dist = new Array(n).fill(0x3f3f3f3f);
dist[x] = 0;
// 有多少个点就迭代多少次
for (let k = 0; k < n; k++) {
// 每次都使用上一次迭代的结果,执行松弛操作
const prev = dist.slice();
for (const e of edges) {
const a = e[0], b = e[1], c = e[2];
dist[b] = Math.min(dist[b], prev[a] + c);
dist[a] = Math.min(dist[a], prev[b] + c);
}
}
return dist;
}
let ans = -1, cnt = n + 10;
for (let i = 0; i < n; i++) {
const dist = bf(i);
let cur = 0;
for (let j = 0; j < n; j++) {
if (i !== j && dist[j] <= distanceThreshold) cur++;
}
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
};
- 时间复杂度:统计答案时,共执行 $n$ 次
Bellman Ford算法,Bellman Ford复杂度为 $O(nm)$,总复杂度为 $O(n^2 \times m)$。整体复杂度为 $O(n^2 \times m)$ - 空间复杂度:$O(n + m)$
SPFA(邻接表)
SPFA 也是一类能够处理「负权边」的单源最短路算法。
最坏情况下,复杂度为 $O(n \times m)$,在特定情况下,其效率优于 Dijkstra 算法,近似 $O(m)$。
基本执行流程如下:
- 用双端队列来维护待更新节点,初始将源点放入队列
每次从队列头中取出一个节点,对其所有相邻节点执行松弛操作
- 若某个相邻节点的最短距离发生了更新,且该节点不在队列中,将它加入队列中
重复以上步骤,直到队列为空
Java 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63class Solution {
int N = 110, M = N * N, INF = 0x3f3f3f3f, idx, n;
int[] he = new int[N], e = new int[M], ne = new int[M], w = new int[M];
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
w[idx] = c;
he[a] = idx++;
}
public int findTheCity(int _n, int[][] edges, int distanceThreshold) {
n = _n;
// 初始化链表头
Arrays.fill(he, -1);
// 存图
for (int[] e : edges) {
int a = e[0], b = e[1], c = e[2];
add(a, b, c); add(b, a, c);
}
// 统计答案
int ans = -1, cnt = n + 10;
for (int i = 0; i < n; i++) {
// 单源最短路
int[] dist = spfa(i);
int cur = 0;
for (int j = 0; j < n; j++) {
if (i != j && dist[j] <= distanceThreshold) cur++;
}
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
}
int[] spfa(int x) {
int[] dist = new int[n];
boolean[] vis = new boolean[n];
// 起始先将所有的点标记为「未入队」和「距离为正无穷」
Arrays.fill(dist, INF);
// 只有起点最短距离为 0
dist[x] = 0;
// 使用「双端队列」存储,存储的是点编号
Deque<Integer> d = new ArrayDeque<>();
// 将「源点/起点」进行入队,并标记「已入队」
d.addLast(x);
vis[x] = true;
while (!d.isEmpty()) {
// 每次从「双端队列」中取出,并标记「未入队」
int u = d.pollFirst();
vis[u] = false;
// 尝试使用该点,更新其他点的最短距离
// 如果更新的点,本身「未入队」则加入队列中,并标记「已入队」
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] <= dist[u] + w[i]) continue;
dist[j] = dist[u] + w[i];
if (vis[j]) continue;
d.addLast(j);
vis[j] = true;
}
}
return dist;
}
}
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57class Solution {
public:
static const int N = 110, M = N * N;
int he[N], e[M], ne[M], w[M], idx, n, INF = 0x3f3f3f3f;
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
w[idx] = c;
he[a] = idx++;
}
int findTheCity(int _n, vector<vector<int>>& edges, int distanceThreshold) {
n = _n;
fill(he, he + N, -1);
for (const auto& e : edges) {
int a = e[0], b = e[1], c = e[2];
add(a, b, c); add(b, a, c);
}
int ans = -1, cnt = n + 10;
for (int i = 0; i < n; i++) {
vector<int> dist = spfa(i);
int cur = count_if(dist.begin(), dist.end(), [&](int d) { return d != INF && d <= distanceThreshold; });
if (cur <= cnt) {
cnt = cur; ans = i;
}
}
return ans;
}
vector<int> spfa(int x) {
// 起始先将所有的点标记为「未入队」和「距离为正无穷」
vector<int> dist(n, INF);
vector<bool> vis(n, false);
// 只有起点最短距离为 0
dist[x] = 0;
// 使用「双端队列」存储,存储的是点编号
deque<int> d;
// 将「源点/起点」进行入队,并标记「已入队」
d.push_back(x);
vis[x] = true;
while (!d.empty()) {
// 每次从「双端队列」中取出,并标记「未入队」
int u = d.front();
d.pop_front();
vis[u] = false;
// 尝试使用该点,更新其他点的最短距离
// 如果更新的点,本身「未入队」则加入队列中,并标记「已入队」
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] <= dist[u] + w[i]) continue;
dist[j] = dist[u] + w[i];
if (vis[j]) continue;
d.push_back(j);
vis[j] = true;
}
}
return dist;
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
m, INF, idx = n * n, 0x3f3f3f3f, 0
he, e, ne, w = [-1] * n, [0] * m, [0] * m, [0] * m
def add(a: int, b: int, c: int):
nonlocal idx
e[idx] = b
ne[idx] = he[a]
w[idx] = c
he[a] = idx
idx += 1
def spfa(x: int) -> List[int]:
# 起始先将所有的点标记为「未入队」和「距离为正无穷」
dist = [INF] * n
vis = [False] * n
# 只有起点最短距离为 0
dist[x] = 0
# 使用「双端队列」存储,存储的是点编号
d = deque()
# 将「源点/起点」进行入队,并标记「已入队」
d.append(x)
vis[x] = True
while d:
# 每次从「双端队列」中取出,并标记「未入队」
u = d.popleft()
vis[u] = False
i = he[u]
# 尝试使用该点,更新其他点的最短距离
# 如果更新的点,本身「未入队」则加入队列中,并标记「已入队」
while i != -1:
j, c = e[i], w[i]
i = ne[i]
if dist[j] <= dist[u] + c: continue
dist[j] = dist[u] + c
if vis[j]: continue
d.append(j)
vis[j] = True
return dist
for a, b, c in edges:
add(a, b, c)
add(b, a, c)
ans, cnt = -1, n + 10
for i in range(n):
dist = spfa(i)
cur = sum(1 for d in dist if d != INF and d <= distanceThreshold)
if cur <= cnt:
cnt, ans = cur, i
return ans
- 时间复杂度:统计答案时,共执行 $n$ 次
spfa算法,spfa复杂度为 $O(nm)$,总复杂度为 $O(n^2 \times m)$。整体复杂度为 $O(n^2 \times m)$ - 空间复杂度:$O(n + m)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.1334 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
