LC 790. 多米诺和托米诺平铺
题目描述
这是 LeetCode 上的 790. 多米诺和托米诺平铺 ,难度为 中等。
有两种形状的瓷砖:一种是 2 x 1 的多米诺形,另一种是形如 "L" 的托米诺形,两种形状都可以旋转。
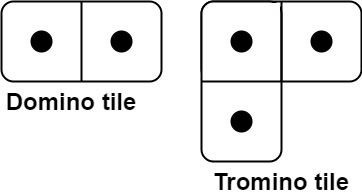
给定整数 n ,返回可以平铺 2 x n 的面板的方法的数量,返回对 $10^9 + 7$ 取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。
两个平铺不同,当且仅当面板上有四个方向上的相邻单元中的两个,使得恰好有一个平铺有一个瓷砖占据两个正方形。
示例 1: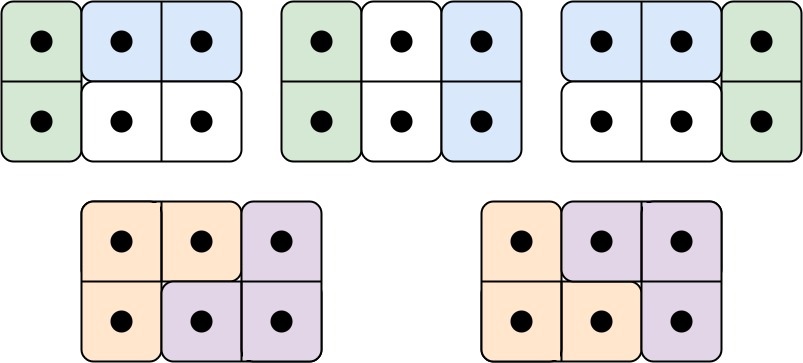
1
2
3
4
5输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
示例 2:1
2
3输入: n = 1
输出: 1
提示:
- $1 <= n <= 1000$
状态机 DP
定义 $f[i][j]$ 为无须考虑前 $i - 1$ 列(含义为前 $i - 1$ 列已铺满),当前第 $i$ 列状态为 $j$ 时的方案数。
其中 $j$ 取值范围为 $[0, 4)$ 分别对应了当前列的填充情况:
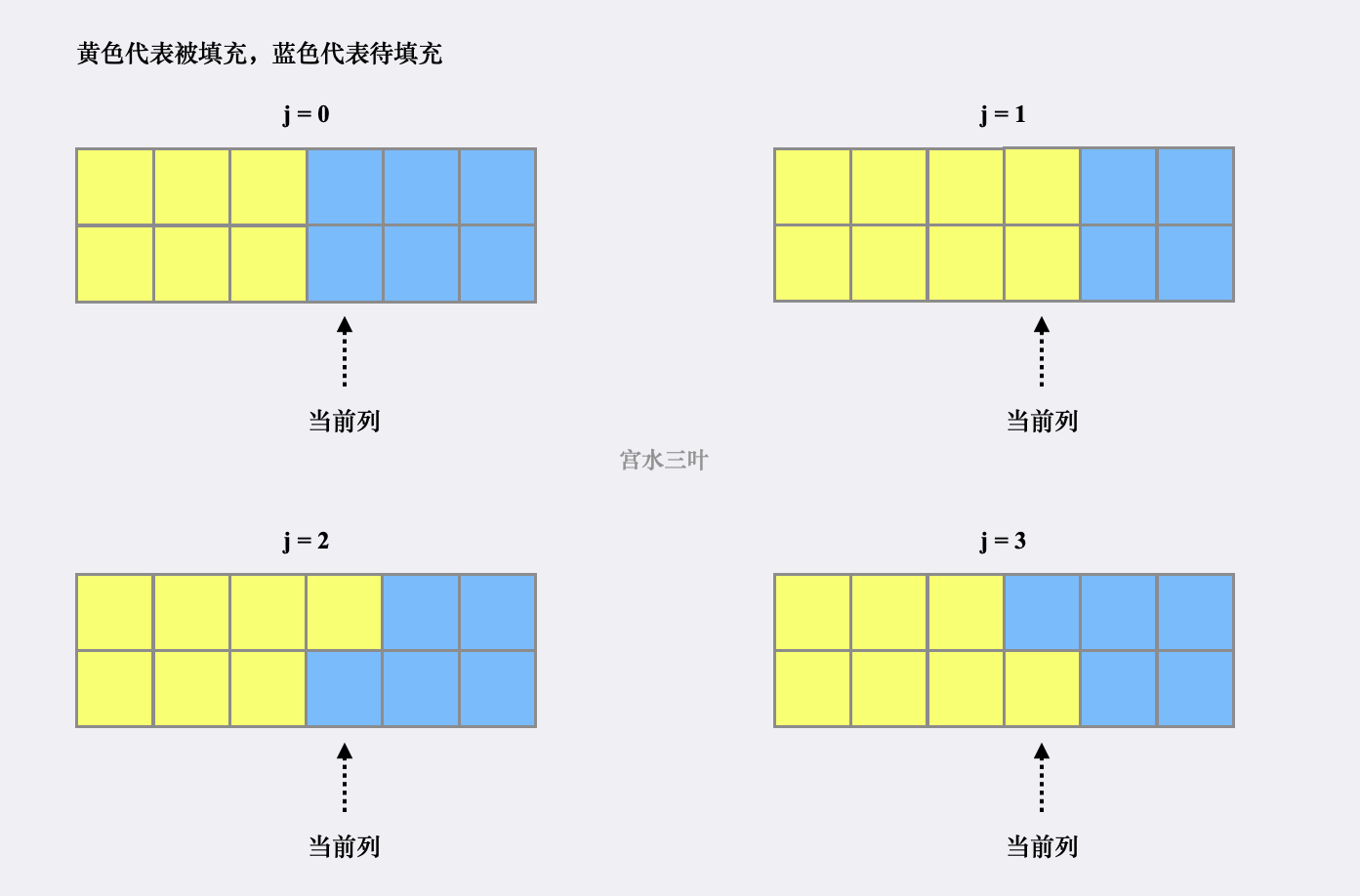
为了方便,我们人为规定列数从 $1$ 开始。
由于骨牌只能在 $2 \times n$ 的棋盘内填充(不能延伸出棋盘两端),因此我们有显而易见的初始化状态:
分别对应「第一列不放置任何骨牌」和「第一列竖着放一块 $1 \times 2$ 骨牌」合法方案。
而 $f[1][2]$ 和 $f[1][3]$ 由于没法在棋盘左侧以外的位置放置骨牌,不存在合法方案,其值均为 $0$。
同时可知 $f[n][1]$ 为我们最终答案,含义为所有列都恰好铺完,不溢出棋盘右侧位置。
不失一般性考虑 $f[i][j]$ 该如何计算,其实就是一个简单的状态机转移分情况讨论:
$f[i][0]$ : 需要前 $i - 1$ 列铺满,同时第 $i$ 列没有被铺,只能由 $f[i - 1][1]$ 转移而来,即有 $f[i][0] = f[i - 1][1]$
这里需要尤其注意:虽然我们能够在上一步留空第 $i - 1$ 列,然后在 $i - 1$ 列竖放一块 $1 \times 2$ 的骨牌(如下图)

但我们不能从 $f[i - 1][0]$ 转移到 $f[i][0]$,因为此时放置的骨牌,仅对第 $i - 1$ 列产生影响,不会对第 $i$ 列产生影响,该决策所产生的方案数,已在 $f[i - 1][X]$ 时被统计
$f[i][1]$ : 可由 $f[i - 1][j]$ 转移而来(见下图),其中 $j \in [0, 4)$,即有 $f[i][1] = \sum_{j = 0}^{3} f[i - 1][j]$
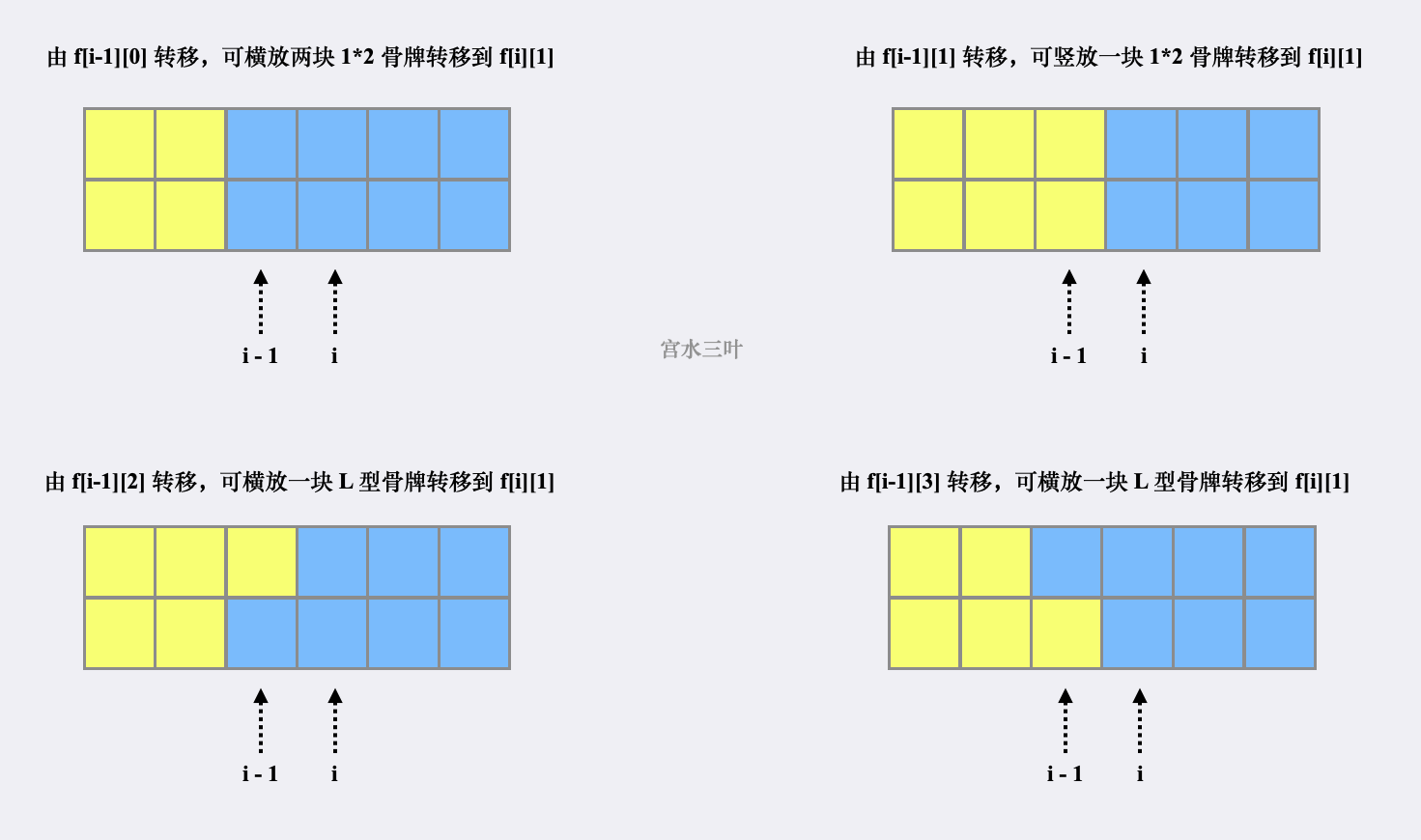
$f[i][2]$ : 可由 $f[i - 1][0]$ 和 $f[i - 1][3]$ 转移而来
$f[i][3]$ : 可由 $f[i - 1][0]$ 和 $f[i - 1][2]$ 转移而来
Java 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
int MOD = (int)1e9+7;
public int numTilings(int n) {
int[][] f = new int[n + 10][4];
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= n; i++) {
f[i][0] = f[i - 1][1];
int cur = 0;
for (int j = 0; j < 4; j++) cur = (cur + f[i - 1][j]) % MOD;
f[i][1] = cur;
f[i][2] = (f[i - 1][0] + f[i - 1][3]) % MOD;
f[i][3] = (f[i - 1][0] + f[i - 1][2]) % MOD;
}
return f[n][1];
}
}
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
const int MOD = 1e9 + 7;
public:
int numTilings(int n){
vector<vector<int>> f(n + 10, vector<int>(4));
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= n; ++i){
f[i][0] = f[i - 1][1];
int cur = 0;
for (int j = 0; j < 4; ++j) cur = (cur + f[i - 1][j]) % MOD;
f[i][1] = cur;
f[i][2] = (f[i - 1][0] + f[i - 1][3]) % MOD;
f[i][3] = (f[i - 1][0] + f[i - 1][2]) % MOD;
}
return f[n][1];
}
};
Python3 代码:1
2
3
4
5
6
7
8
9
10class Solution:
def numTilings(self, n: int) -> int:
f = [[0] * 4 for _ in range(n + 10)]
f[1][0] = f[1][1] = 1
for i in range(2, n + 1):
f[i][0] = f[i - 1][1]
f[i][1] = sum([f[i - 1][j] for j in range(4)])
f[i][2] = f[i - 1][0] + f[i - 1][3]
f[i][3] = f[i - 1][0] + f[i - 1][2]
return f[n][1] % 1000000007
TypeScript 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15function numTilings(n: number): number {
const MOD = 1e9+7
const f = new Array<Array<number>>()
for (let i = 0; i <= n; i++) f[i] = new Array<number>(4).fill(0)
f[1][0] = f[1][1] = 1
for (let i = 2; i <= n; i++) {
f[i][0] = f[i - 1][1]
let cur = 0
for (let j = 0; j < 4; j++) cur = (cur + f[i - 1][j]) % MOD
f[i][1] = cur
f[i][2] = (f[i - 1][0] + f[i - 1][3]) % MOD
f[i][3] = (f[i - 1][0] + f[i - 1][2]) % MOD
}
return f[n][1]
}
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
滚动数组优化
利用 $f[i][X]$ 仅依赖于 $f[i - 1][X]$,我们可以采用「滚动数组」方式将其空间优化至 $O(1)$。
Java 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
int MOD = (int)1e9+7;
public int numTilings(int n) {
int[][] f = new int[2][4];
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= n; i++) {
int a = i & 1, b = (i - 1) & 1;
f[a][0] = f[b][1];
int cur = 0;
for (int j = 0; j < 4; j++) cur = (cur + f[b][j]) % MOD;
f[a][1] = cur;
f[a][2] = (f[b][0] + f[b][3]) % MOD;
f[a][3] = (f[b][0] + f[b][2]) % MOD;
}
return f[n & 1][1];
}
}
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
const int MOD = 1e9 + 7;
public:
int numTilings(int n){
vector<vector<int>> f(2, vector<int>(4));
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= n; ++i){
int a = i & 1, b = (i - 1) & 1;
f[a][0] = f[b][1];
int cur = 0;
for (int j = 0; j < 4; ++j) cur = (cur + f[b][j]) % MOD;
f[a][1] = cur;
f[a][2] = (f[b][0] + f[b][3]) % MOD;
f[a][3] = (f[b][0] + f[b][2]) % MOD;
}
return f[n & 1][1];
}
};
Python3 代码:1
2
3
4
5
6
7
8
9
10
11class Solution:
def numTilings(self, n: int) -> int:
f = [[0] * 4 for _ in range(2)]
f[1][0] = f[1][1] = 1
for i in range(2, n + 1):
a, b = i & 1, (i - 1) & 1
f[a][0] = f[b][1]
f[a][1] = sum([f[b][j] for j in range(4)])
f[a][2] = f[b][0] + f[b][3]
f[a][3] = f[b][0] + f[b][2]
return f[n & 1][1] % 1000000007
TypeScript 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16function numTilings(n: number): number {
const MOD = 1e9+7
const f = new Array<Array<number>>()
for (let i = 0; i <= 1; i++) f[i] = new Array<number>(4).fill(0)
f[1][0] = f[1][1] = 1
for (let i = 2; i <= n; i++) {
const a = i & 1, b = (i - 1) & 1
f[a][0] = f[b][1]
let cur = 0
for (let j = 0; j < 4; j++) cur = (cur + f[b][j]) % MOD
f[a][1] = cur
f[a][2] = (f[b][0] + f[b][3]) % MOD
f[a][3] = (f[b][0] + f[b][2]) % MOD
}
return f[n & 1][1]
}
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.790 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
