LC 655. 输出二叉树
题目描述
这是 LeetCode 上的 655. 输出二叉树 ,难度为 中等。
给你一棵二叉树的根节点 root,请你构造一个下标从 0 开始、大小为 $m \times n$ 的字符串矩阵 res,用以表示树的格式化布局。
构造此格式化布局矩阵需要遵循以下规则:
- 树的高度为
height,矩阵的行数m应该等于 $height + 1$。 - 矩阵的列数
n应该等于 $2^{height+1 - 1}$ 。 - 根节点需要放置在顶行的正中间,对应位置为 $res[0][(n-1)/2]$ 。
- 对于放置在矩阵中的每个节点,设对应位置为 $res[r][c]$ ,将其左子节点放置在 $res[r+1][c-2^{height-r-1}]$ ,右子节点放置在 $res[r+1][c+2^{height-r-1}]$ 。
- 继续这一过程,直到树中的所有节点都妥善放置。
- 任意空单元格都应该包含空字符串
""。
返回构造得到的矩阵 res 。
示例 1:
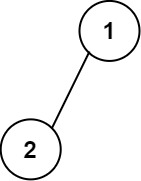
1 | |
示例 2:
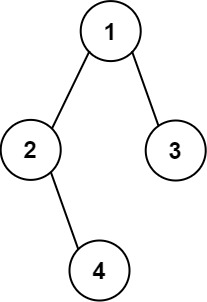
1 | |
提示:
- 树中节点数在范围 $[1, 2^{10}]$ 内
- $-99 <= Node.val <= 99$
- 树的深度在范围 $[1, 10]$ 内
DFS
根据题意,我们可以先设计 dfs1 递归函数得到树的高度 h,以及与其相关的矩阵行列大小(并初始化矩阵)。
随后根据填充规则,设计 dfs2 递归函数往矩阵进行填充。
注意:在位移操作中,C++ 和 Python 不允许负值移位量,需要额外处理一下。
Java 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
int h, m, n;
List<List<String>> ans;
public List<List<String>> printTree(TreeNode root) {
dfs1(root, 0);
m = h + 1; n = (1 << (h + 1)) - 1;
ans = new ArrayList<>();
for (int i = 0; i < m; i++) {
List<String> cur = new ArrayList<>();
for (int j = 0; j < n; j++) cur.add("");
ans.add(cur);
}
dfs2(root, 0, (n - 1) / 2);
return ans;
}
void dfs1(TreeNode root, int depth) {
if (root == null) return ;
h = Math.max(h, depth);
dfs1(root.left, depth + 1);
dfs1(root.right, depth + 1);
}
void dfs2(TreeNode root, int x, int y) {
if (root == null) return ;
ans.get(x).set(y, String.valueOf(root.val));
dfs2(root.left, x + 1, y - (1 << (h - x - 1)));
dfs2(root.right, x + 1, y + (1 << (h - x - 1)));
}
}
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
int h = 0, m, n;
vector<vector<string>> ans;
public:
vector<vector<string>> printTree(TreeNode* root) {
dfs1(root, 0);
m = h + 1;
n = (1 << (h + 1)) - 1;
ans = vector<vector<string>>(m, vector<string>(n, ""));
dfs2(root, 0, (n - 1) / 2);
return ans;
}
void dfs1(TreeNode* root, int depth) {
if (!root) return;
h = max(h, depth);
dfs1(root->left, depth + 1);
dfs1(root->right, depth + 1);
}
void dfs2(TreeNode* root, int x, int y) {
if (!root) return;
ans[x][y] = to_string(root->val);
if (h - x - 1 >= 0) {
dfs2(root->left, x + 1, y - (1 << (h - x - 1)));
dfs2(root->right, x + 1, y + (1 << (h - x - 1)));
}
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution:
def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:
self.h = 0
self.dfs1(root, 0)
m = self.h + 1
n = (1 << (self.h + 1)) - 1
self.ans = [["" for _ in range(n)] for _ in range(m)]
self.dfs2(root, 0, (n - 1) // 2)
return self.ans
def dfs1(self, root: TreeNode, depth: int) -> None:
if not root:
return
self.h = max(self.h, depth)
self.dfs1(root.left, depth + 1)
self.dfs1(root.right, depth + 1)
def dfs2(self, root: TreeNode, x: int, y: int) -> None:
if not root:
return
self.ans[x][y] = str(root.val)
if self.h - x - 1 >= 0:
shift = 1 << (self.h - x - 1)
if y - shift >= 0:
self.dfs2(root.left, x + 1, y - shift)
if y + shift < len(self.ans[0]):
self.dfs2(root.right, x + 1, y + shift)
Typescript 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25let h: number, m: number, n: number;
let ans: string[][];
function printTree(root: TreeNode | null): string[][] {
h = 0
dfs1(root, 0)
m = h + 1; n = (1 << (h + 1)) - 1
ans = new Array<Array<string>>()
for (let i = 0; i < m; i++) {
ans[i] = new Array<string>(n).fill("")
}
dfs2(root, 0, (n - 1) / 2)
return ans
};
function dfs1(root: TreeNode | null, depth: number): void {
if (root == null) return
h = Math.max(h, depth)
dfs1(root.left, depth + 1)
dfs1(root.right, depth + 1)
}
function dfs2(root: TreeNode | null, x: number, y: number): void {
if (root == null) return
ans[x][y] = root.val + "";
dfs2(root.left, x + 1, y - (1 << (h - x - 1)))
dfs2(root.right, x + 1, y + (1 << (h - x - 1)))
}
- 时间复杂度:$O(n \times m)$
- 空间复杂度:$O(n \times m)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.655 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
