LC 450. 删除二叉搜索树中的节点
题目描述
这是 LeetCode 上的 450. 删除二叉搜索树中的节点 ,难度为 中等。
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
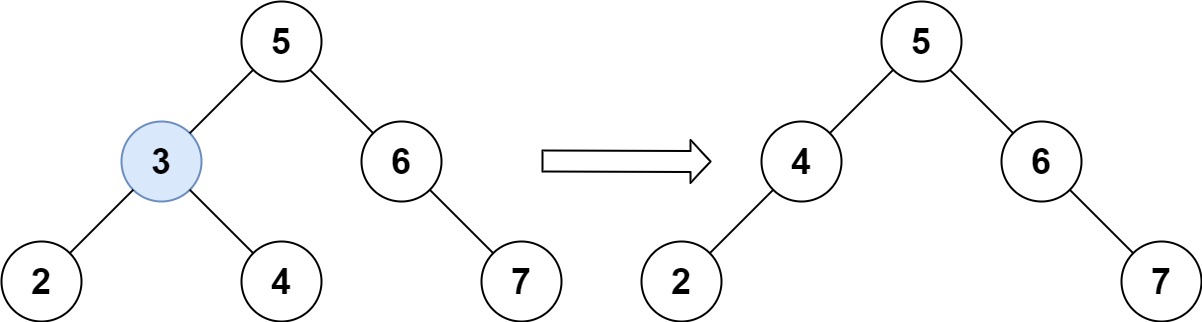
1 | |
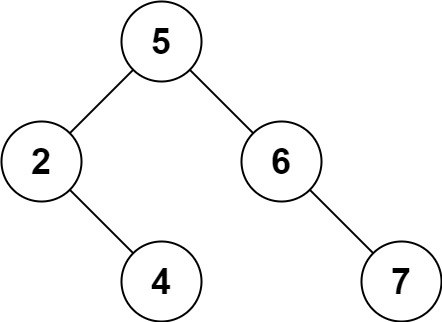
1 | |
示例 2:1
2
3
4
5输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:1
2
3输入: root = [], key = 0
输出: []
提示:
- 节点数的范围 $[0, 10^4]$
- $-10^5 <= Node.val <= 10^5$
- 节点值唯一
- root 是合法的二叉搜索树
- $-10^5 <= key <= 10^5$
进阶: 要求算法时间复杂度为 $O(h)$,$h$ 为树的高度。
递归
利用题目本身的函数签名的含义,也就是「在以 root 为根的子树中,删除值为 key 的节点,并返回删除节点后的树的根节点」,我们可以用「递归」来做。
起始先对边界情况进行处理,当 root 为空(可能起始传入的 root 为空,也可能是递归过程中没有找到值为 key 的节点时,导致的 root 为空),我们无须进行任何删除,直接返回 null 即可。
根据当前 root.val 与 key 的大小关系,进行分情况讨论:
- 若有 $root.val < key$,说明待删除的节点必然不是当前节点,以及不在当前节点的左子树中,我们将删除动作「递归」到当前节点的右子树,并将删除(可能进行)之后的新的右子树根节点,重新赋值给
root.right,即有root.right = deleteNode(root.right, key); - 若有 $root.val > key$,说明待删除的节点必然不是当前节点,以及不在当前节点的右子树,我们将删除节点「递归」到当前节点的左子树,并将删除(可能进行)之后的新的左子树根节点,重新赋值给
root.left,即有root.left = deleteNode(root.left, key); 若有 $root.val = key$,此时找到了待删除的节点,我们根据左右子树的情况,进行进一步分情况讨论:
- 若左/右子树为空,我们直接返回右/左子树节点即可(含义为直接将右/左子树节点搬到当前节点的位置)如图所示:
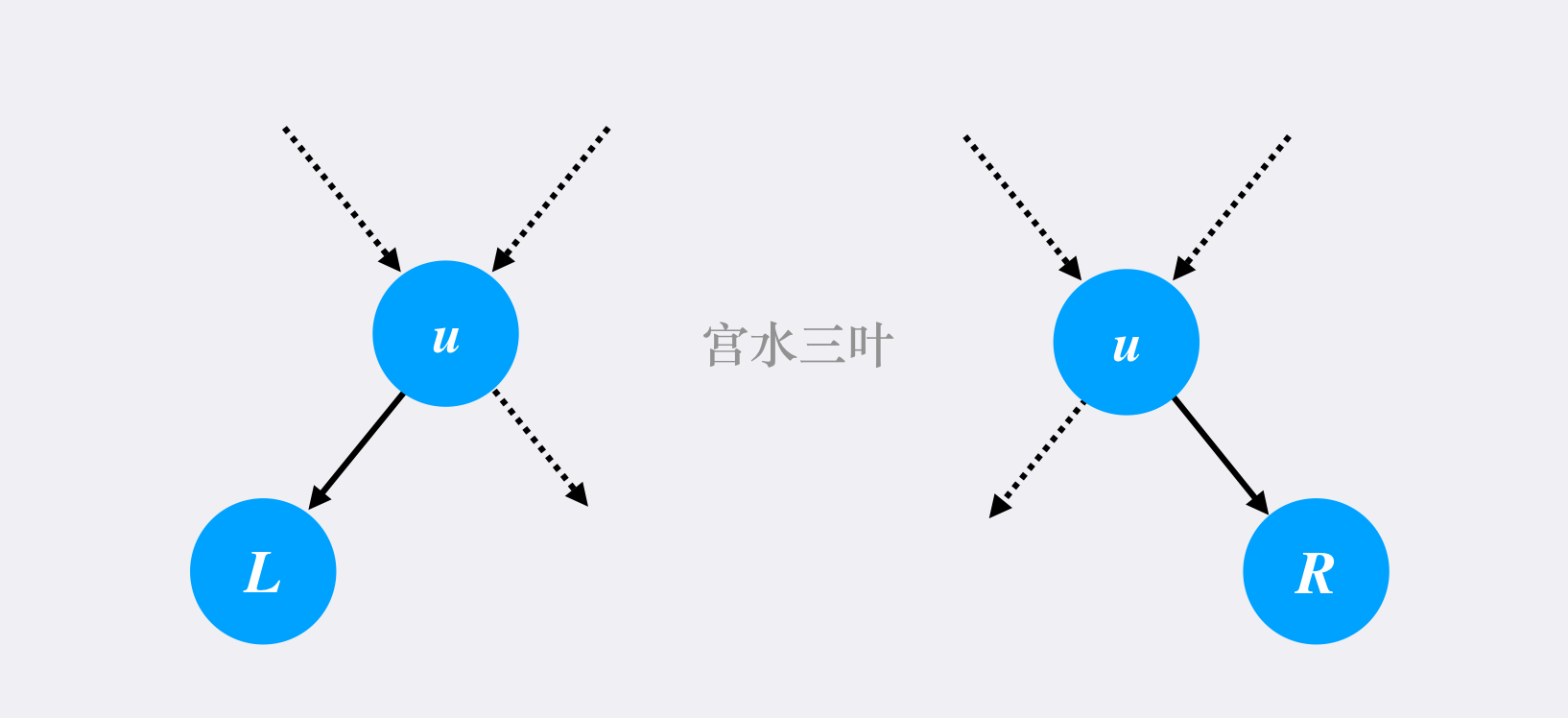
若左右子树均不为空,我们有两种选择:
- 从「当前节点的左子树」中选择「值最大」的节点替代
root的位置,确保替代后仍满足BST特性; 从「当前节点的右子树」中选择「值最小」的节点替代
root的位置,确保替代后仍满足BST特性;我们以「从当前节点的左子树中选择值最大的节点」为例子,我们通过树的遍历,找到其位于「最右边」的节点,记为 $t$($t$ 作为最右节点,必然有
t.right = null),利用原本的root也是合法BST,原本的root.right子树的所有及节点,必然满足大于t.val,我们可以直接将root.right接在t.right上,并返回我们重接后的根节点,也就是root.left。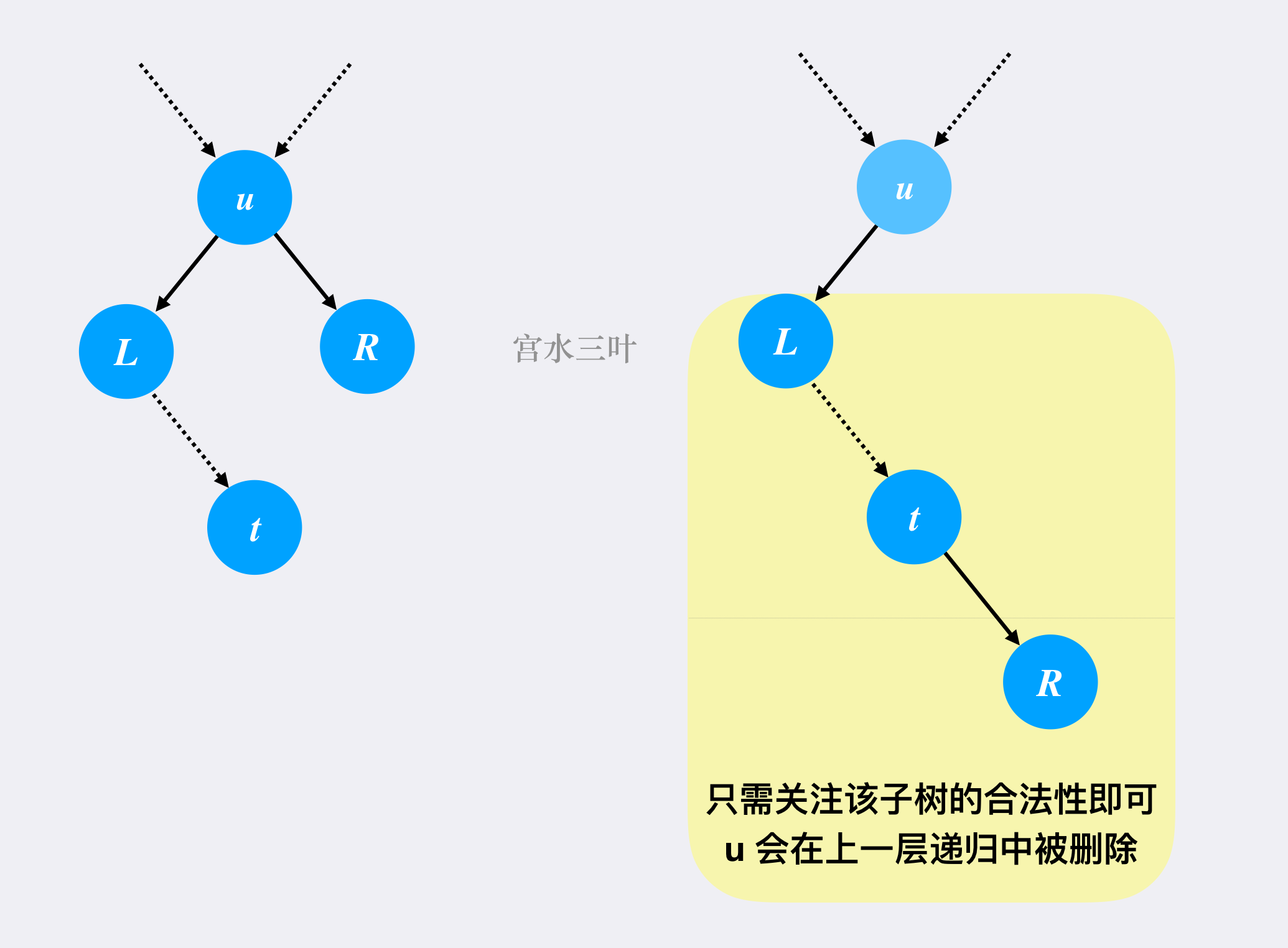
而「从当前节点的右子树中选择值最小的节点」,同理(代码见 $P2$)。
- 从「当前节点的左子树」中选择「值最大」的节点替代
- 若左/右子树为空,我们直接返回右/左子树节点即可(含义为直接将右/左子树节点搬到当前节点的位置)如图所示:
Java 代码(P1):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
if (root.left == null) return root.right;
if (root.right == null) return root.left;
TreeNode t = root.left;
while (t.right != null) t = t.right;
t.right = root.right;
return root.left;
} else if (root.val < key) root.right = deleteNode(root.right, key);
else root.left = deleteNode(root.left, key);
return root;
}
}
Java 代码(P2):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
if (root.left == null) return root.right;
if (root.right == null) return root.left;
TreeNode t = root.right;
while (t.left != null) t = t.left;
t.left = root.left;
return root.right;
} else if (root.val < key) root.right = deleteNode(root.right, key);
else root.left = deleteNode(root.left, key);
return root;
}
}
C++ 代码(P1):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (!root) return nullptr;
if (root->val == key) {
if (!root->left) return root->right;
if (!root->right) return root->left;
TreeNode* t = root->left;
while (t->right) t = t->right;
t->right = root->right;
return root->left;
} else if (root->val < key) {
root->right = deleteNode(root->right, key);
} else {
root->left = deleteNode(root->left, key);
}
return root;
}
};
Python 代码(P1):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root:
return None
if root.val == key:
if not root.left:
return root.right
if not root.right:
return root.left
t = root.left
while t.right:
t = t.right
t.right = root.right
return root.left
elif root.val < key:
root.right = self.deleteNode(root.right, key)
else:
root.left = self.deleteNode(root.left, key)
return root
TypeScript 代码(P1):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16function deleteNode(root: TreeNode | null, key: number): TreeNode | null {
if (!root) return null;
if (root.val === key) {
if (!root.left) return root.right;
if (!root.right) return root.left;
let t: TreeNode | null = root.left;
while (t!.right) t = t!.right;
t!.right = root.right;
return root.left;
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
} else {
root.left = deleteNode(root.left, key);
}
return root;
};
- 时间复杂度:$O(h)$,其中 $h$ 为树的深度
- 空间复杂度:忽略递归带来的额外空间消耗,复杂度为 $O(1)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.450 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
