LC 427. 建立四叉树
题目描述
这是 LeetCode 上的 427. 建立四叉树 ,难度为 中等。
给你一个 $n \times n$ 矩阵 grid ,矩阵由若干 $0$ 和 $1$ 组成。请你用四叉树表示该矩阵 grid 。
你需要返回能表示矩阵的 四叉树 的根结点。
注意,当 isLeaf 为 False 时,你可以把 True 或者 False 赋值给节点,两种值都会被判题机制 接受 。
四叉树数据结构中,每个内部节点只有四个子节点。此外,每个节点都有两个属性:
val:储存叶子结点所代表的区域的值。$1$ 对应True,$0$ 对应False;isLeaf: 当这个节点是一个叶子结点时为True,如果它有 $4$ 个子节点则为False。我们可以按以下步骤为二维区域构建四叉树:1
2
3
4
5
6
7
8class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
- 如果当前网格的值相同(即,全为 $0$ 或者全为 $1$),将
isLeaf设为True,将val设为网格相应的值,并将四个子节点都设为Null然后停止。 - 如果当前网格的值不同,将
isLeaf设为False, 将val设为任意值,然后如下图所示,将当前网格划分为四个子网格。 - 使用适当的子网格递归每个子节点。
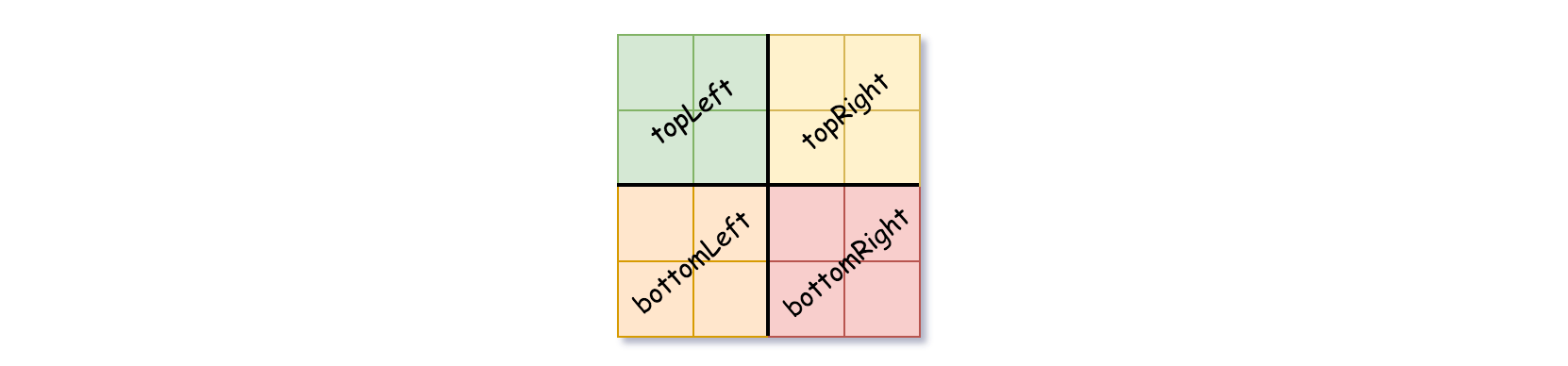
四叉树格式:
输出为使用层序遍历后四叉树的序列化形式,其中 null 表示路径终止符,其下面不存在节点。
它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 $[isLeaf, val]$ 。
如果 isLeaf 或者 val 的值为 True ,则表示它在列表 $[isLeaf, val]$ 中的值为 $1$ ;如果 isLeaf 或者 val 的值为 False ,则表示值为 $0$ 。
示例 1: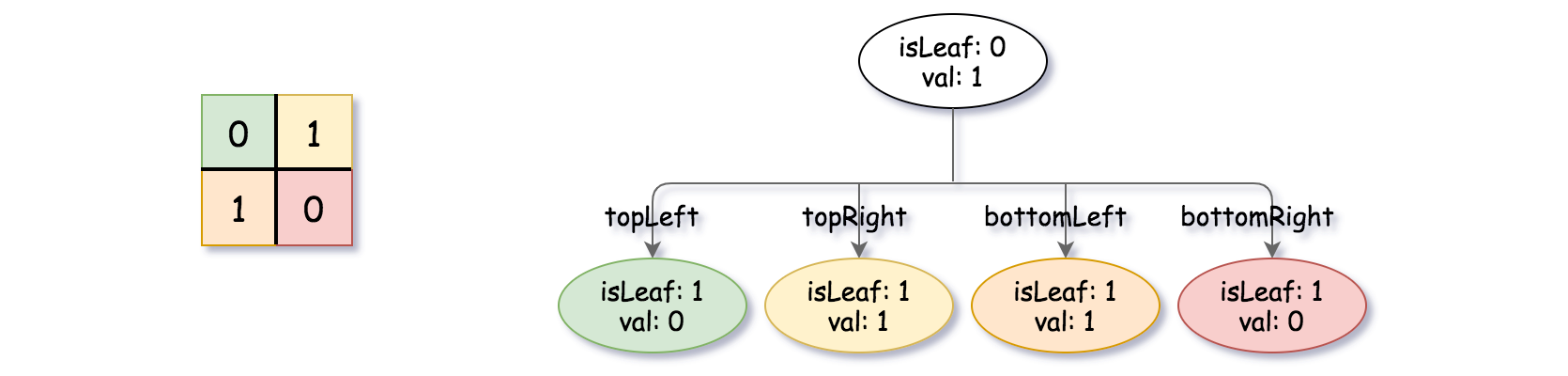
1
2
3
4
5输入:grid = [[0,1],[1,0]]
输出:[[0,1],[1,0],[1,1],[1,1],[1,0]]
解释:请注意,在下面四叉树的图示中,0 表示 false,1 表示 True 。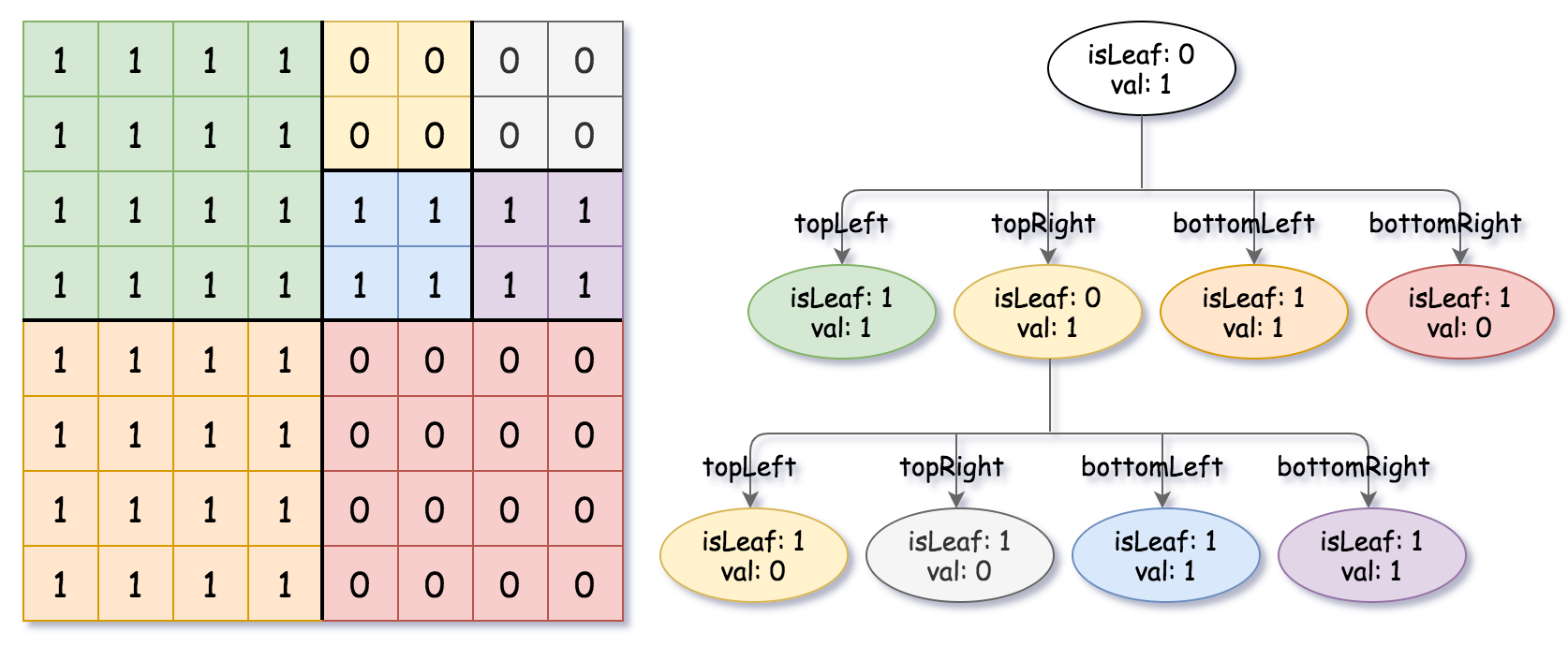
示例 2:
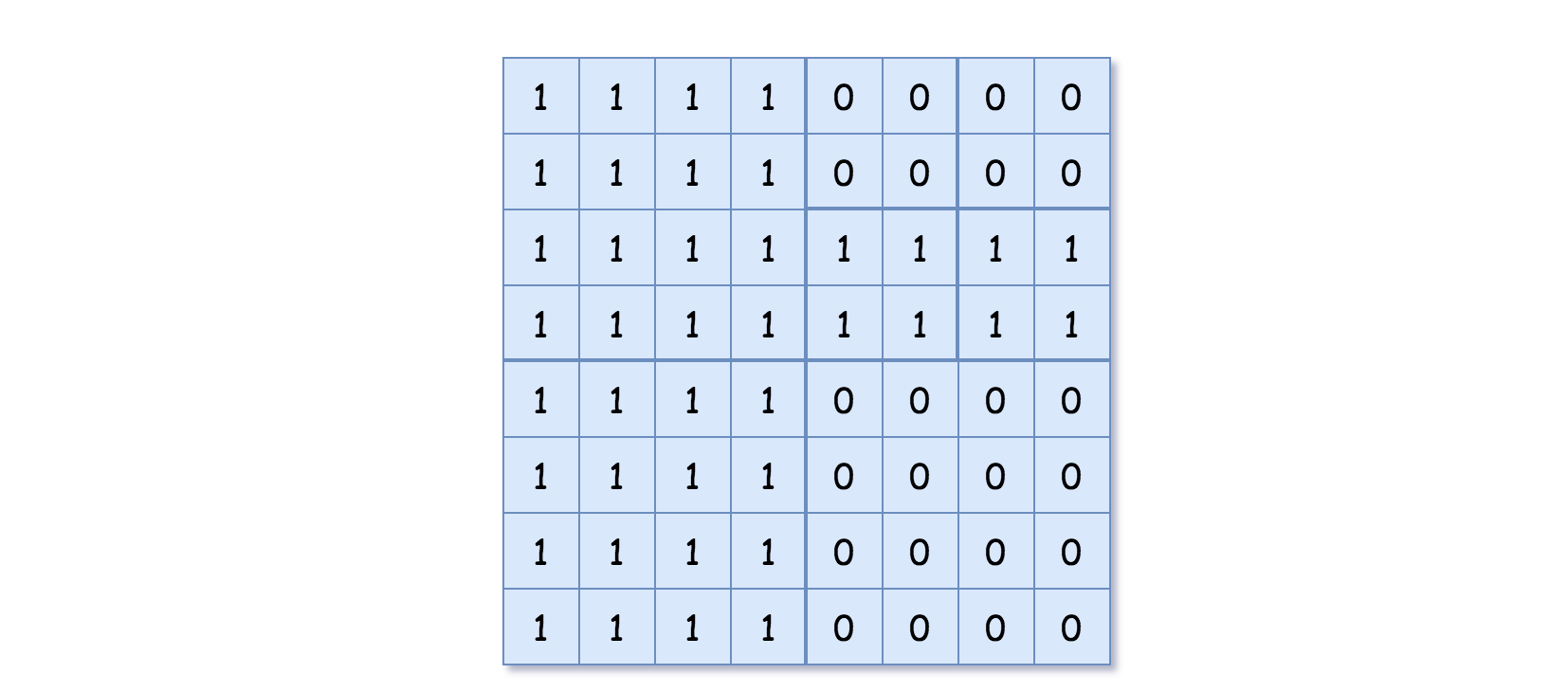
1 | |
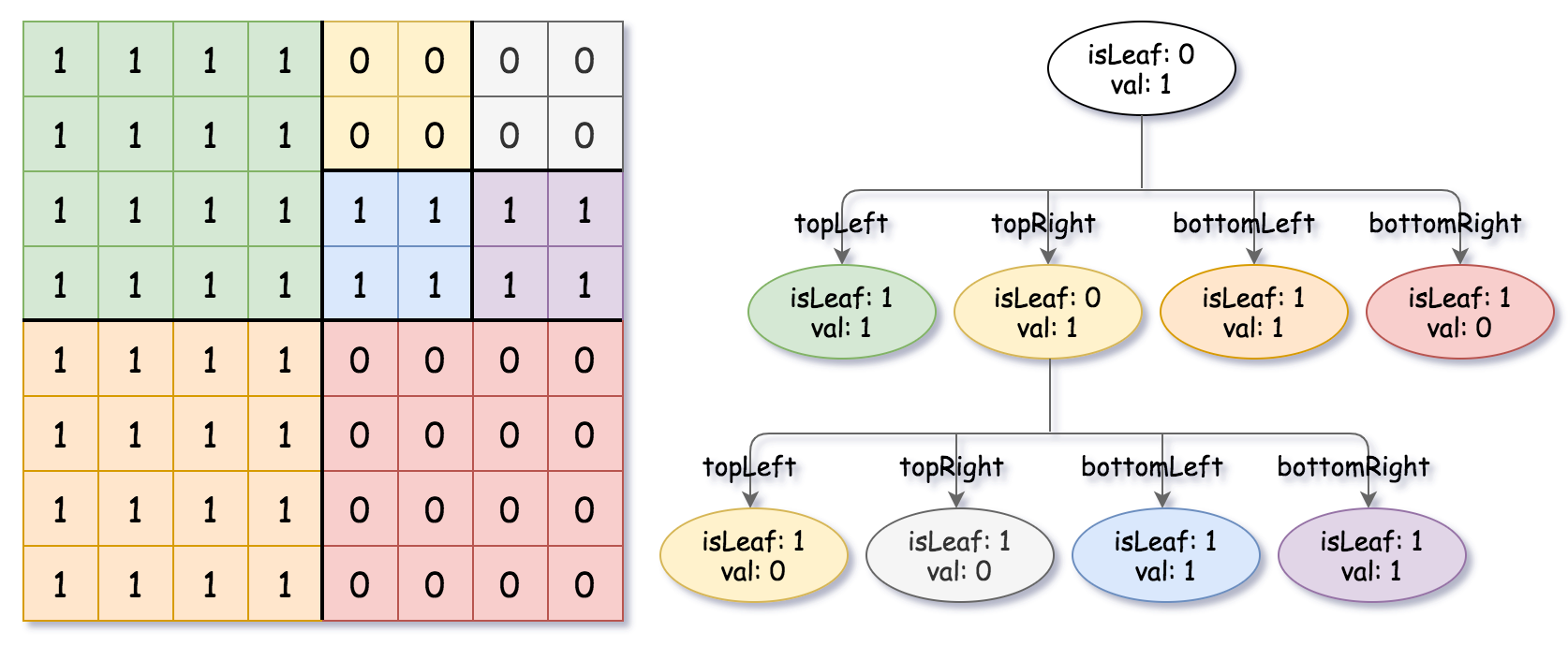
示例 3:
1 | |
示例 4:1
2
3输入:grid = [[0]]
输出:[[1,0]]
示例 5:1
2
3输入:grid = [[1,1,0,0],[1,1,0,0],[0,0,1,1],[0,0,1,1]]
输出:[[0,1],[1,1],[1,0],[1,0],[1,1]]
提示:
- $n == grid.length == grid[i].length$
- $n == 2^x$ 其中 $0 <= x <= 6$
递归
假定我们存在函数 Node dfs(int a, int b, int c, int d),其能够返回「以 $(a, b)$ 为左上角,$(c, d)$ 为右下角」所代表的矩阵的根节点。
那么最终答案为 dfs(0, 0, n-1, n-1),不失一般性考虑「以 $(a, b)$ 为左上角,$(c, d)$ 为右下角」时如何计算:
- 判断该矩阵是否为全 $0$ 或全 $1$:
- 如果是则直接创建根节点(该节点四个子节点属性均为空)并进行返回;
- 如果不是则创建根节点,递归创建四个子节点并进行赋值,利用左上角 $(a,b)$ 和右下角 $(c, d)$ 可算的横纵坐标的长度为 $c - a + 1$ 和 $d - b + 1$,从而计算出将当前矩阵四等分所得到的子矩阵的左上角和右下角坐标。
由于矩阵大小最多为 $2^6 = 64$ ,因此判断某个子矩阵是否为全 $0$ 或全 $1$ 的操作用「前缀和」或者是「暴力」来做都可以。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
int[][] g;
public Node construct(int[][] grid) {
g = grid;
return dfs(0, 0, g.length - 1, g.length - 1);
}
Node dfs(int a, int b, int c, int d) {
boolean ok = true;
int t = g[a][b];
for (int i = a; i <= c && ok; i++) {
for (int j = b; j <= d && ok; j++) {
if (g[i][j] != t) ok = false;
}
}
if (ok) return new Node(t == 1, true);
Node root = new Node(t == 1, false);
int dx = c - a + 1, dy = d - b + 1;
root.topLeft = dfs(a, b, a + dx / 2 - 1, b + dy / 2 - 1);
root.topRight = dfs(a, b + dy / 2, a + dx / 2 - 1, d);
root.bottomLeft = dfs(a + dx / 2, b, c, b + dy / 2 - 1);
root.bottomRight = dfs(a + dx / 2, b + dy / 2, c, d);
return root;
}
}
- 时间复杂度:递归的复杂度分析要根据主定理,假设矩阵大小为 $n \times n$,根据主定理 $T(n) = aT(\frac{n}{b}) + f(n)$,单次递归最多会产生 $4$ 个子问题(由大矩阵递归 $4$ 个小矩阵),因此问题递归子问题数量 $a = 4$,而子问题规模缩减系数 $b$ 为原本的一半(子矩阵的大小为 $\frac{n}{2} \times \frac{n}{2}$),剩余的 $f(n)$ 为判断全 $0$ 和 全 $1$ 的时间开销,不考虑标识位 $ok$ 带来的剪枝效果,每次判断全 $0$ 或全 $1$ 的复杂度与当前问题规模相等,即 $f(n) = O(n^2)$,但整个大小为 $n \times n$ 矩阵每次进行长宽减半的子矩阵拆分,最多会被拆分为 $\log{n}$ 次,因此这部分总的计算量为 $\log{n} \times n^2$ 。整体复杂度为 $O(n^2 + \log{n} \times n^2)$
- 空间复杂度:忽略递归带来的额外空间开销,复杂度为 $O(1)$
递归(前缀和优化)
使用前缀和优化「判断全 $0$ 和全 $1$」的操作:对矩阵 grid 求前缀和数组 sum,对于一个「以左上角为 $(a, b)$,右下角为 $(c, d)$ 」的子矩阵而言,其所包含的格子总数为 $tot = (c - a + 1) * (d - b + 1)$ 个,当且仅当矩阵和为 $0$ 或 $tot$ 时,矩阵全 $0$ 或 $1$。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
static int[][] sum = new int[70][70];
int[][] g;
public Node construct(int[][] grid) {
g = grid;
int n = grid.length;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + g[i - 1][j - 1];
}
}
return dfs(0, 0, n - 1, n - 1);
}
Node dfs(int a, int b, int c, int d) {
int cur = sum[c + 1][d + 1] - sum[a][d + 1] - sum[c + 1][b] + sum[a][b];
int dx = c - a + 1, dy = d - b + 1, tot = dx * dy;
if (cur == 0 || cur == tot) return new Node(g[a][b] == 1, true);
Node root = new Node(g[a][b] == 1, false);
root.topLeft = dfs(a, b, a + dx / 2 - 1, b + dy / 2 - 1);
root.topRight = dfs(a, b + dy / 2, a + dx / 2 - 1, d);
root.bottomLeft = dfs(a + dx / 2, b, c, b + dy / 2 - 1);
root.bottomRight = dfs(a + dx / 2, b + dy / 2, c, d);
return root;
}
}
- 时间复杂度:分析同理,但判断全 $0$ 和全 $1$ 的复杂度下降为 $O(1)$,整体复杂度为 $O(n^2 + \log{n})$
- 空间复杂度:忽略递归带来的额外空间开销,复杂度为 $O(n^2)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.427 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
