LC 417. 太平洋大西洋水流问题
题目描述
这是 LeetCode 上的 417. 太平洋大西洋水流问题 ,难度为 中等。
有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , $heights[r][c]$ 表示坐标 $(r, c)$ 上单元格 高于海平面的高度 。
岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回 网格坐标 result 的 2D 列表 ,其中 $result[i] = [r_i, c_i]$ 表示雨水可以从单元格 $(r_i, c_i)$ 流向 太平洋和大西洋 。
示例 1: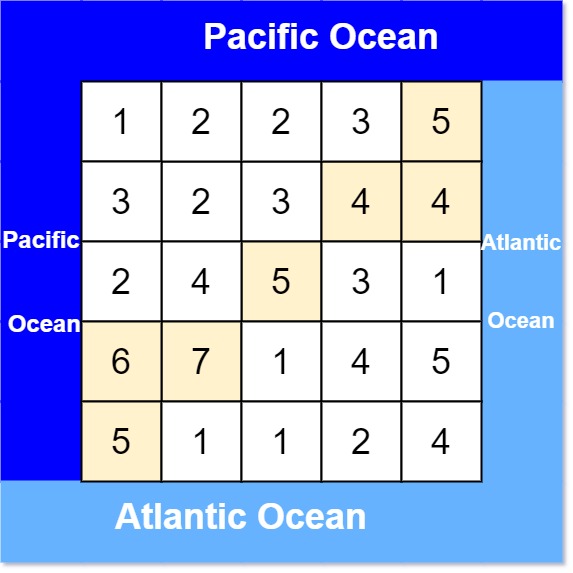
1
2
3输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例 2:1
2
3输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]
提示:
- $m == heights.length$
- $n == heights[r].length$
- $1 <= m, n <= 200$
- $0 <= heights[r][c] <= 10^5$
基本分析
整理题意,需要我们统计能够同时流向两片海域的格子。
从源点(格子)流向汇点(海域)是按照高度从高到低(非严格)的规则,那么反过来从海域到格子则是按照从低到高(非严格)规则进行,同时本身处于边缘的格子与海域联通。
因此我们可以使用两遍 DFS/BFS 进行求解:分别从与当前海域直接相连的边缘格子出发,统计能够流向当前海域的格子集合,两片海域求得的集合交集即是答案。
BFS(多源 BFS)
使用 BFS 进行求解:目的是构造出两个答案矩阵 $res_1$ 和 $res_2$,$res_k[i][j] = true$ 代表格子 $(i, j)$ 能够流向海域,起始将所有与海域相连的格子放入队列,然后跑一遍 BFS ,所有能够进入队列的格子均能够与海域联通。
最后统计所有满足 $res_1[i][j] = res_2[i][j] = true$ 的格子即是答案。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48class Solution {
int n, m;
int[][] g;
public List<List<Integer>> pacificAtlantic(int[][] heights) {
g = heights;
m = g.length; n = g[0].length;
Deque<int[]> d1 = new ArrayDeque<>(), d2 = new ArrayDeque<>();
boolean[][] res1 = new boolean[m][n], res2 = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 || j == 0) {
res1[i][j] = true;
d1.addLast(new int[]{i, j});
}
if (i == m - 1 || j == n - 1) {
res2[i][j] = true;
d2.addLast(new int[]{i, j});
}
}
}
bfs(d1, res1); bfs(d2, res2);
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (res1[i][j] && res2[i][j]) {
List<Integer> list = new ArrayList<>();
list.add(i); list.add(j);
ans.add(list);
}
}
}
return ans;
}
int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
void bfs(Deque<int[]> d, boolean[][] res) {
while (!d.isEmpty()) {
int[] info = d.pollFirst();
int x = info[0], y = info[1], t = g[x][y];
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1];
if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
if (res[nx][ny] || g[nx][ny] < t) continue;
d.addLast(new int[]{nx, ny});
res[nx][ny] = true;
}
}
}
}
- 时间复杂度:
BFS和统计答案的复杂度均为 $O(m \times n)$。整体复杂度为 $O(m \times n)$ - 空间复杂度:$O(m \times n)$
DFS
同理,使用 DFS 进行求解。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution {
int n, m;
int[][] g;
public List<List<Integer>> pacificAtlantic(int[][] heights) {
g = heights;
m = g.length; n = g[0].length;
boolean[][] res1 = new boolean[m][n], res2 = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 || j == 0) {
if (!res1[i][j]) dfs(i, j, res1);
}
if (i == m - 1 || j == n - 1) {
if (!res2[i][j]) dfs(i, j, res2);
}
}
}
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (res1[i][j] && res2[i][j]) {
List<Integer> list = new ArrayList<>();
list.add(i); list.add(j);
ans.add(list);
}
}
}
return ans;
}
int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
void dfs(int x, int y, boolean[][] res) {
res[x][y] = true;
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1];
if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
if (res[nx][ny] || g[nx][ny] < g[x][y]) continue;
dfs(nx, ny, res);
}
}
}
- 时间复杂度:
DFS和统计答案的复杂度均为 $O(m \times n)$。整体复杂度为 $O(m \times n)$ - 空间复杂度:$O(m \times n)$
并查集
其中维护连通性部分可以使用「并查集」来做:起始将与海域 A 联通的边缘格子与 S 联通,将与海域 B 联通的边缘格子与 T 联通,然后跑一遍 DFS/BFS,最后将既和 S 联通又和 T 联通的格子加入答案。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57class Solution {
int N = 200 * 200 + 10;
int[] p1 = new int[N], p2 = new int[N];
int n, m, tot, S, T;
int[][] g;
void union(int[] p, int a, int b) {
p[find(p, a)] = p[find(p, b)];
}
int find(int[] p, int x) {
if (p[x] != x) p[x] = find(p, p[x]);
return p[x];
}
boolean query(int[] p, int a, int b) {
return find(p, a) == find(p, b);
}
int getIdx(int x, int y) {
return x * n + y;
}
public List<List<Integer>> pacificAtlantic(int[][] _g) {
g = _g;
m = g.length; n = g[0].length; tot = m * n; S = tot + 1; T = tot + 2;
for (int i = 0; i <= T; i++) p1[i] = p2[i] = i;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int idx = getIdx(i, j);
if (i == 0 || j == 0) {
if (!query(p1, S, idx)) dfs(p1, S, i, j);
}
if (i == m - 1 || j == n - 1) {
if (!query(p2, T, idx)) dfs(p2, T, i, j);
}
}
}
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int idx = getIdx(i, j);
if (query(p1, S, idx) && query(p2, T, idx)) {
List<Integer> list = new ArrayList<>();
list.add(i); list.add(j);
ans.add(list);
}
}
}
return ans;
}
int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
void dfs(int[] p, int ori, int x, int y) {
union(p, ori, getIdx(x, y));
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1];
if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
if (query(p, ori, getIdx(nx, ny)) || g[nx][ny] < g[x][y]) continue;
dfs(p, ori, nx, ny);
}
}
}
- 时间复杂度:$O(n \times m)$
- 空间复杂度:$O(n \times m)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.417 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
