LC 587. 安装栅栏
题目描述
这是 LeetCode 上的 587. 安装栅栏 ,难度为 困难。
在一个二维的花园中,有一些用 $(x, y)$ 坐标表示的树。由于安装费用十分昂贵,你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时,花园才能围好栅栏。
你需要找到正好位于栅栏边界上的树的坐标。
示例 1: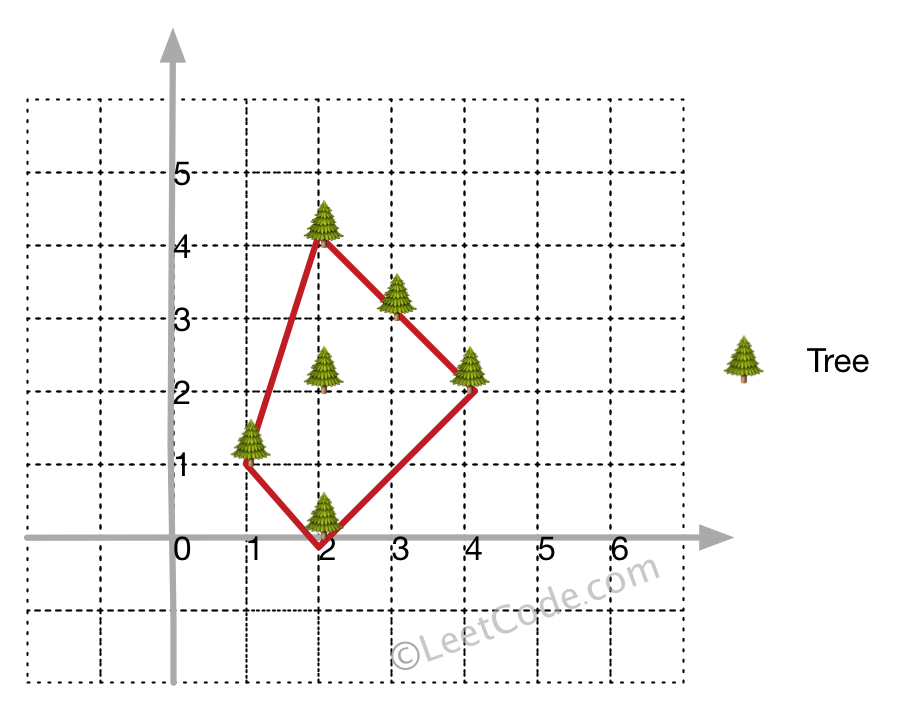
1
2
3
4输入: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
输出: [[1,1],[2,0],[4,2],[3,3],[2,4]]
示例 2: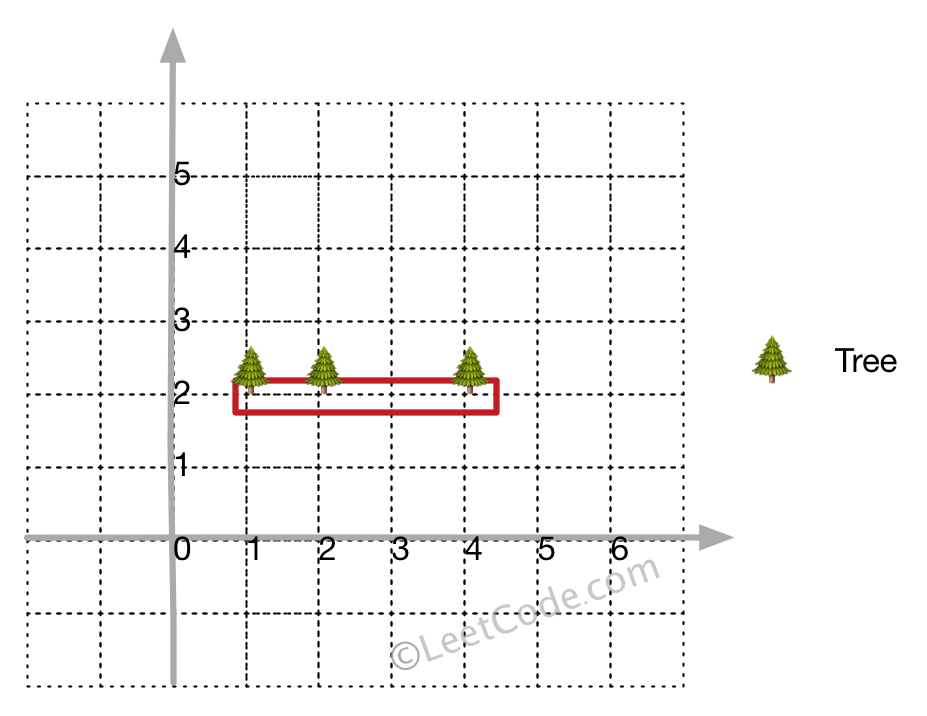
1
2
3
4
5输入: [[1,2],[2,2],[4,2]]
输出: [[1,2],[2,2],[4,2]]
解释:即使树都在一条直线上,你也需要先用绳子包围它们。
注意:
- 所有的树应当被围在一起。你不能剪断绳子来包围树或者把树分成一组以上。
- 输入的整数在 $0$ 到 $100$ 之间。
- 花园至少有一棵树。
- 所有树的坐标都是不同的。
- 输入的点没有顺序。输出顺序也没有要求。
二维凸包(Andrew 算法)
这是一道「二维凸包」板子题,需要注意的是网上大多数 Andrew 算法的板子都是有问题的(下面会说)。
Andrew 算法正是用于求解凸包上的所有点(围成所有点的最小周长),其算法逻辑将凸包分为「上凸壳」和「下凸壳」,并分别画出(蓝色分割线将凸包分为两部分):
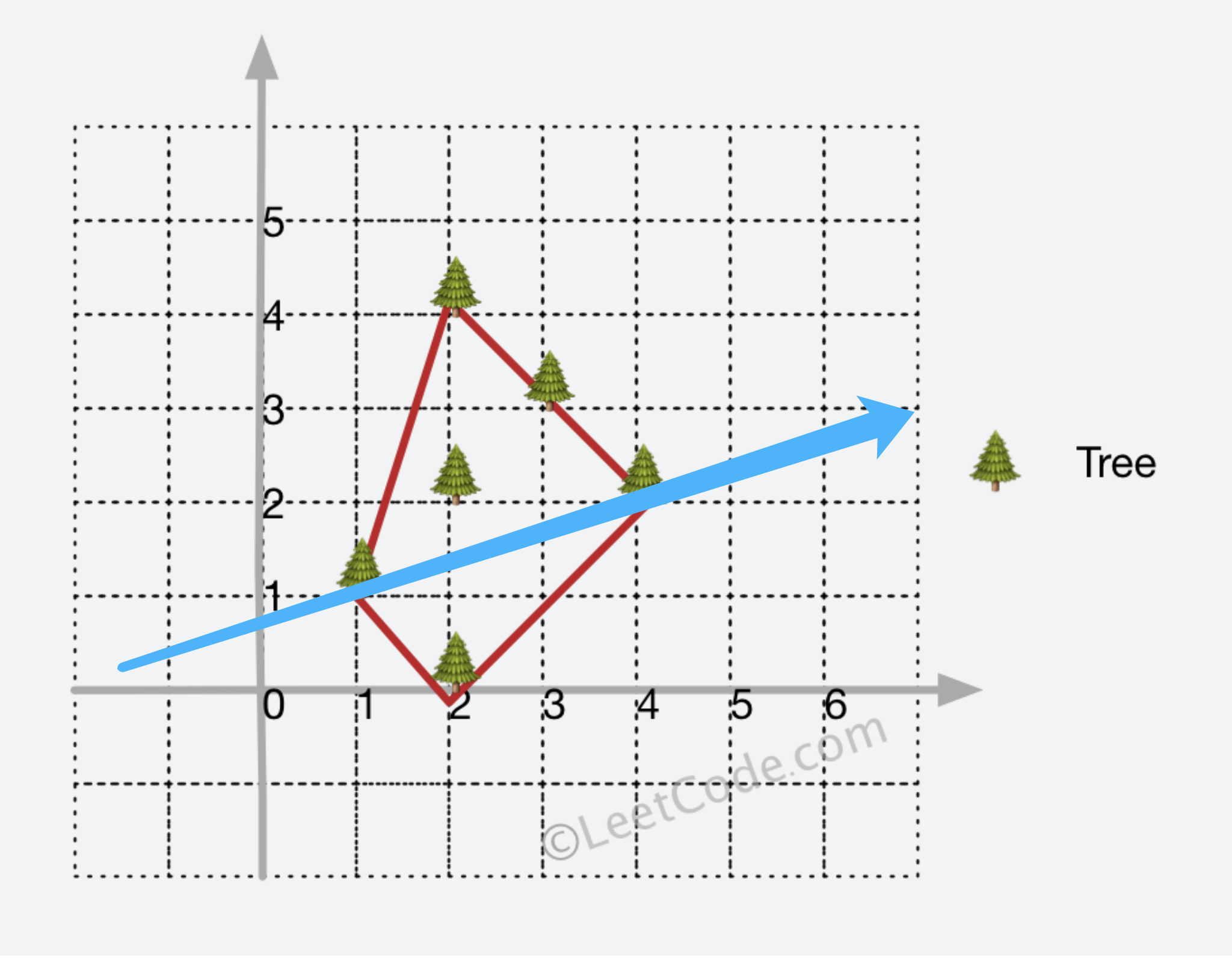
基本流程为:
对所有点进行双关键字排序,先根据 $x$ 坐标排升序,后根据 $y$ 排升序;
根据 $x$ 排升序的目的,是为了我们能够往一个方向画出凸包边缘(从左往后画出一半凸壳,从右往左画出另外一半),而将 $y$ 升序目的是可以确保一旦我们现在从 $a$ 到 $b$ 进行连线,那么 $a$ 到 $b$ 之间的所有点能够确保被围住;使用栈来维护所有凸包上的点,或者说凸包上的边,会更为准确,凸包起点元素会在栈中出现两次(首尾),因此更为准确的描述应该是使用栈维护凸包的所有的边,栈中相邻元素代表凸包上的一条边;
分别「从前往后」和「从后往前」处理排序好的所有点,来分别画出凸包的两半部分,根据画的是第一部分还是第二部分,维护栈内元的处理逻辑稍有不同:
a. 画的是凸包的第一部分:
- 若栈内元素少于 $2$ 个,组成一条线至少需要两个点,说明此时第一条边都还没画出,直接将元素添加到栈中;
若栈内元素不少于 $2$ 个,考虑是否要将栈顶的边删掉(由栈顶前两个元素组成的边)假设栈顶元素为 $b$,栈顶元素的下一位为 $a$,即栈顶存在一条 $a$ 到 $b$ 的边,当前处理到的点为 $c$,此时我们根据 $ac$ 边是否在 $ab$ 边的时针方向来决定是否要将 $ab$ 边去掉:

按照上述逻辑处理完所有点,凸包第一部分的点(边)都存在于栈中。
b. 画的是凸包的第二部分:逻辑同理,唯一需要注意的是,第一部分的凸包边我们不能删去,假定处理完第一部分凸包,我们栈内有 $m$ 个元素,我们需要将上述「栈顶元素不少于 $2$ 个」的逻辑替换为「栈顶元素大于 $m$ 个」,同时已参与到凸包第一部分的点,不能再考虑,因此需要额外使用一个 $vis$ 数组来记录使用过的点。
一些细节,为了方便取得栈顶的前两位元素,我们使用数组实现栈,$stk$ 代表栈容器,$tp$ 代表栈顶元素下标。
正如刚刚讲到,起点会被入栈两次(对应第一条边和最后一条边),因此输出方案时,栈顶和栈底我们只选其一即可。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46class Solution {
int[] subtraction(int[] a, int[] b) { // 向量相减
return new int[]{a[0] - b[0], a[1] - b[1]};
}
double cross(int[] a, int[] b) { // 叉乘
return a[0] * b[1] - a[1] * b[0];
}
double getArea(int[] a, int[] b, int[] c) { // 向量 ab 转为 向量 ac 过程中扫过的面积
return cross(subtraction(b, a), subtraction(c, a));
}
public int[][] outerTrees(int[][] trees) {
Arrays.sort(trees, (a, b)->{
return a[0] != b[0] ? a[0] - b[0] : a[1] - b[1];
});
int n = trees.length, tp = 0;
int[] stk = new int[n + 10];
boolean[] vis = new boolean[n + 10];
stk[++tp] = 0; // 不标记起点
for (int i = 1; i < n; i++) {
int[] c = trees[i];
while (tp >= 2) {
int[] a = trees[stk[tp - 1]], b = trees[stk[tp]];
if (getArea(a, b, c) > 0) vis[stk[tp--]] = false;
else break;
}
stk[++tp] = i;
vis[i] = true;
}
int size = tp;
for (int i = n - 1; i >= 0; i--) {
if (vis[i]) continue;
int[] c = trees[i];
while (tp > size) {
int[] a = trees[stk[tp - 1]], b = trees[stk[tp]];
if (getArea(a, b, c) > 0) tp--;
// vis[stk[tp--]] = false; // 非必须
else break;
}
stk[++tp] = i;
// vis[i] = true; // 非必须
}
int[][] ans = new int[tp - 1][2];
for (int i = 1; i < tp; i++) ans[i - 1] = trees[stk[i]];
return ans;
}
}
- 时间复杂度:排序复杂度为 $O(n\log{n})$,统计凸包上的点复杂度为 $O(n)$。整体复杂度为 $O(n)$
- 空间复杂度:$O(n)$
网上 Andrew 板子问题
由于我太久没写计算几何了,翻了一下以前在其他 OJ 提交的题,找回自己几年前的板子,好奇心驱使,想看看现在是否有板子上的突破(通常很难,尤其对于计算几何而言),结果发现网上绝大多数板子都存在严重逻辑错误:
- 最为严重的错误是,处理凸包第一部分和第二部分,都是使用「栈顶元素不少于 $2$ 个」的逻辑:即使存在 $vis$ 数组也无法避免该逻辑错误,在某些数据上,该逻辑会导致最右边的一些点无法被围住;
- 存在对
vis数组的错误理解:vis的作用仅是为了处理凸包第二部分的时候,不要使用到凸包第一部分的点而已。含义并非是处理过的点,或者当前凸包上的点,因此你可以看到我代码注释中写了「不标记起点」和「非必须」,在画第二部分的凸包时,只需要确保第一部分使用的点不参与即可,重复点问题本身就由遍历所保证,而并非 $vis$ 数组。当然,为了记忆方便,让模板更具有“对称性”,也可以保留在画第二部分凸包的时候,保留对 $vis$ 的维护逻辑,但千万不要搞错了 $vis$ 的含义。
最后
这是我们「刷穿 LeetCode」系列文章的第 No.587 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
