LC 2039. 网络空闲的时刻
题目描述
这是 LeetCode 上的 2039. 网络空闲的时刻 ,难度为 中等。
给你一个有 $n$ 个服务器的计算机网络,服务器编号为 $0$ 到 $n - 1$ 。同时给你一个二维整数数组 edges ,其中 $edges[i] = [u_i, v_i]$ 表示服务器 $u_i$ 和 $v_i$ 之间有一条信息线路,在一秒内它们之间可以传输任意数目的信息。再给你一个长度为 $n$ 且下标从 $0$ 开始的整数数组 patience 。
题目保证所有服务器都是相通的,也就是说一个信息从任意服务器出发,都可以通过这些信息线路直接或间接地到达任何其他服务器。
编号为 $0$ 的服务器是主服务器,其他服务器为数据服务器。每个数据服务器都要向主服务器发送信息,并等待回复。信息在服务器之间按最优线路传输,也就是说每个信息都会以最少时间到达主服务器。主服务器会处理所有新到达的信息并立即按照每条信息来时的路线反方向发送回复信息。
在 $0$ 秒的开始,所有数据服务器都会发送各自需要处理的信息。从第 $1$ 秒开始,每一秒最开始时,每个数据服务器都会检查它是否收到了主服务器的回复信息(包括新发出信息的回复信息):
- 如果还没收到任何回复信息,那么该服务器会周期性重发信息。数据服务器 $i$ 每 $patience[i]$ 秒都会重发一条信息,也就是说,数据服务器 $i$ 在上一次发送信息给主服务器后的 $patience[i]$ 秒 后 会重发一条信息给主服务器。
- 否则,该数据服务器不会重发信息。
当没有任何信息在线路上传输或者到达某服务器时,该计算机网络变为空闲状态。
请返回计算机网络变为空闲状态的最早秒数。
示例 1: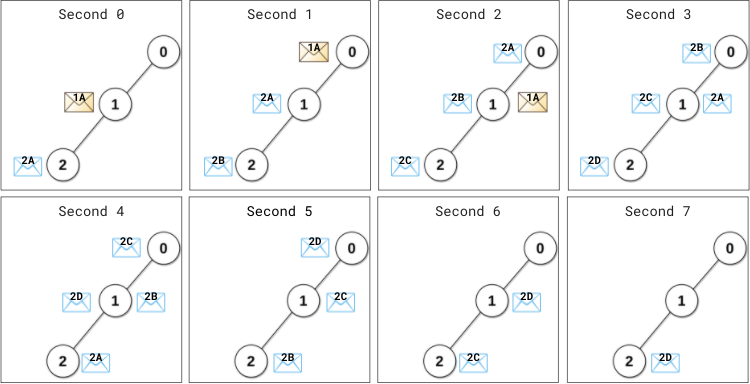
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26输入:edges = [[0,1],[1,2]], patience = [0,2,1]
输出:8
解释:
0 秒最开始时,
- 数据服务器 1 给主服务器发出信息(用 1A 表示)。
- 数据服务器 2 给主服务器发出信息(用 2A 表示)。
1 秒时,
- 信息 1A 到达主服务器,主服务器立刻处理信息 1A 并发出 1A 的回复信息。
- 数据服务器 1 还没收到任何回复。距离上次发出信息过去了 1 秒(1 < patience[1] = 2),所以不会重发信息。
- 数据服务器 2 还没收到任何回复。距离上次发出信息过去了 1 秒(1 == patience[2] = 1),所以它重发一条信息(用 2B 表示)。
2 秒时,
- 回复信息 1A 到达服务器 1 ,服务器 1 不会再重发信息。
- 信息 2A 到达主服务器,主服务器立刻处理信息 2A 并发出 2A 的回复信息。
- 服务器 2 重发一条信息(用 2C 表示)。
...
4 秒时,
- 回复信息 2A 到达服务器 2 ,服务器 2 不会再重发信息。
...
7 秒时,回复信息 2D 到达服务器 2 。
从第 8 秒开始,不再有任何信息在服务器之间传输,也不再有信息到达服务器。
所以第 8 秒是网络变空闲的最早时刻。
示例 2:
1
2
3
4
5
6输入:edges = [[0,1],[0,2],[1,2]], patience = [0,10,10]
输出:3
解释:数据服务器 1 和 2 第 2 秒初收到回复信息。
从第 3 秒开始,网络变空闲。
提示:
- $n == patience.length$
- $2 <= n <= 10^5$
- $patience[0] == 0$
- 对于 $1 <= i < n$ ,满足 $1 <= patience[i] <= 10^5$
- $1 <= edges.length <= \min(105, n * (n - 1) / 2)$
- $edges[i].length == 2$
- $0 <= ui, vi < n$
- $ui != vi$
- 不会有重边。
- 每个服务器都直接或间接与别的服务器相连。
建图 + BFS
根据题目可知这是一个边权为 $1$ 的无向连通图,我们可以采用「邻接表建图 + BFS」的方式预处理出 $dist$ 数组,$dist[i]$ 含义为节点 $i$ 到 $0$ 号点的最短距离。
一个数据服务器 $i$ 往主服务器发送消息所消耗的时间为两节点之间的最短路径 $dist[i]$,而从发送消息到收到回复所需的时间为 $di = 2 * dist[i]$。
同时每个数据服务器还存在时间间隔为 $t = patience[i]$ 的重发动作,并且动作只有在第一次收到主服务的回复后才会停止。
因此如果 $di <= t$,那么数据服务器不会发生重发动作,该节点活动停止时间点为 $di$;当 $di > t$,数据服务器将会发生重发动作,且最后一个数据包的发送时间为 $(di - 1) / t t$,只有当最后一个数据包收到回复,该节点的所有活动才算停止,停止时间点为 $(di - 1) / t t + di$。所有节点的活动停止时间点的最大值即是答案。
一些细节:老规矩,为了避免每个样例都
new大数组,我们使用static优化。使用static优化后,你甚至会收获一个稳定 $100$% 的结果 🤣
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
static int N = 100010, M = N * 2, INF = 0x3f3f3f3f;
static int[] he = new int[N], e = new int[M], ne = new int[M];
static int[] dist = new int[N];
int idx;
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
public int networkBecomesIdle(int[][] edges, int[] patience) {
Arrays.fill(he, -1);
Arrays.fill(dist, INF);
int n = patience.length;
for (int[] e : edges) {
add(e[0], e[1]);
add(e[1], e[0]);
}
Deque<Integer> d = new ArrayDeque<>();
d.addLast(0);
dist[0] = 0;
while (!d.isEmpty()) {
int t = d.pollFirst();
for (int i = he[t]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] != INF) continue;
dist[j] = dist[t] + 1;
d.addLast(j);
}
}
int ans = 0;
for (int i = 1; i < n; i++) {
int di = dist[i] * 2, t = patience[i];
int cur = di <= t ? di : (di - 1) / t * t + di;
if (cur > ans) ans = cur;
}
return ans + 1;
}
}
- 时间复杂度:$O(n + m)$
- 空间复杂度:$O(n + m)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.2039 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
