LC 1036. 逃离大迷宫

题目描述

这是 LeetCode 上的 1036. 逃离大迷宫 ，难度为 困难。

在一个 $10^6 \times 10^6$ 的网格中，每个网格上方格的坐标为 $(x, y)$ 。

现在从源方格 $source = [s_x, s_y]$ 开始出发，意图赶往目标方格 $target = [t_x, t_y]$ 。

数组 $blocked$ 是封锁的方格列表，其中每个 $blocked[i] = [x_i, y_i]$ 表示坐标为 $(x_i, y_i)$ 的方格是禁止通行的。

每次移动，都可以走到网格中在四个方向上相邻的方格，只要该方格 不 在给出的封锁列表 $blocked$ 上。同时，不允许走出网格。

只有在可以通过一系列的移动从源方格 $source$ 到达目标方格 $target$ 时才返回 $true$。否则，返回 $false$。

示例 1：

输入：blocked = [[0,1],[1,0]], source = [0,0], target = [0,2]

输出：false

解释：
从源方格无法到达目标方格，因为我们无法在网格中移动。
无法向北或者向东移动是因为方格禁止通行。
无法向南或者向西移动是因为不能走出网格。

示例 2：

输入：blocked = [], source = [0,0], target = [999999,999999]

输出：true

解释：
因为没有方格被封锁，所以一定可以到达目标方格。

提示：

• $0 <= blocked.length <= 200$
• $blocked[i].length == 2$
• $0 <= xi, yi < 10^6$
• $source.length == target.length == 2$
• $0 <= sx, sy, tx, ty < 10^6$
• $source != target$
• 题目数据保证 $source$ 和 $target$ 不在封锁列表内

---

BFS + 给定障碍物所能围成的最大面积

为了方便，我们用 $s$ 代指 $source$，用 $t$ 代指 $target$，用 $n$ 来代指 $blocked$ 大小。

整理题意为：在一个足够大的空间里，有少数的障碍物，问两点是否连通。

当两点相隔较远时，常规的 BFS 做法可能会搜完整个棋盘，而棋盘大小为 $10^6 \times 10^6$，会 TLE。

考虑什么情况下两点会不连通？

当两个点中的任意一点被障碍物围住时，两点将无法连通。

一个很容易想到的思路是：从 $s$ 跑一遍 BFS，然后从 $t$ 跑一遍 BFS，同时设定一个最大访问点数量 MAX，若从两者出发能够访问的点数量都能超过 MAX，说明两点均没有被围住，最终必然会联通。

考虑如何敲定 MAX 的取值范围？直观感受，MAX 应该是一个与 $blocked$ 大小相关的数。

但第一反应还是想从单秒计算量上界进行反推，两边 BFS 的复杂度均为 $O(\max)$，因此直接设定 MAX = 1e5 应该是比较合适的。

更小的 MAX 需要证明：在给定数量障碍物的前提下，障碍物所能围成的最大面积为多少。

首先，容易想到：任何一条封闭图形的直边都可以通过调整为斜边来围成更大的面积：

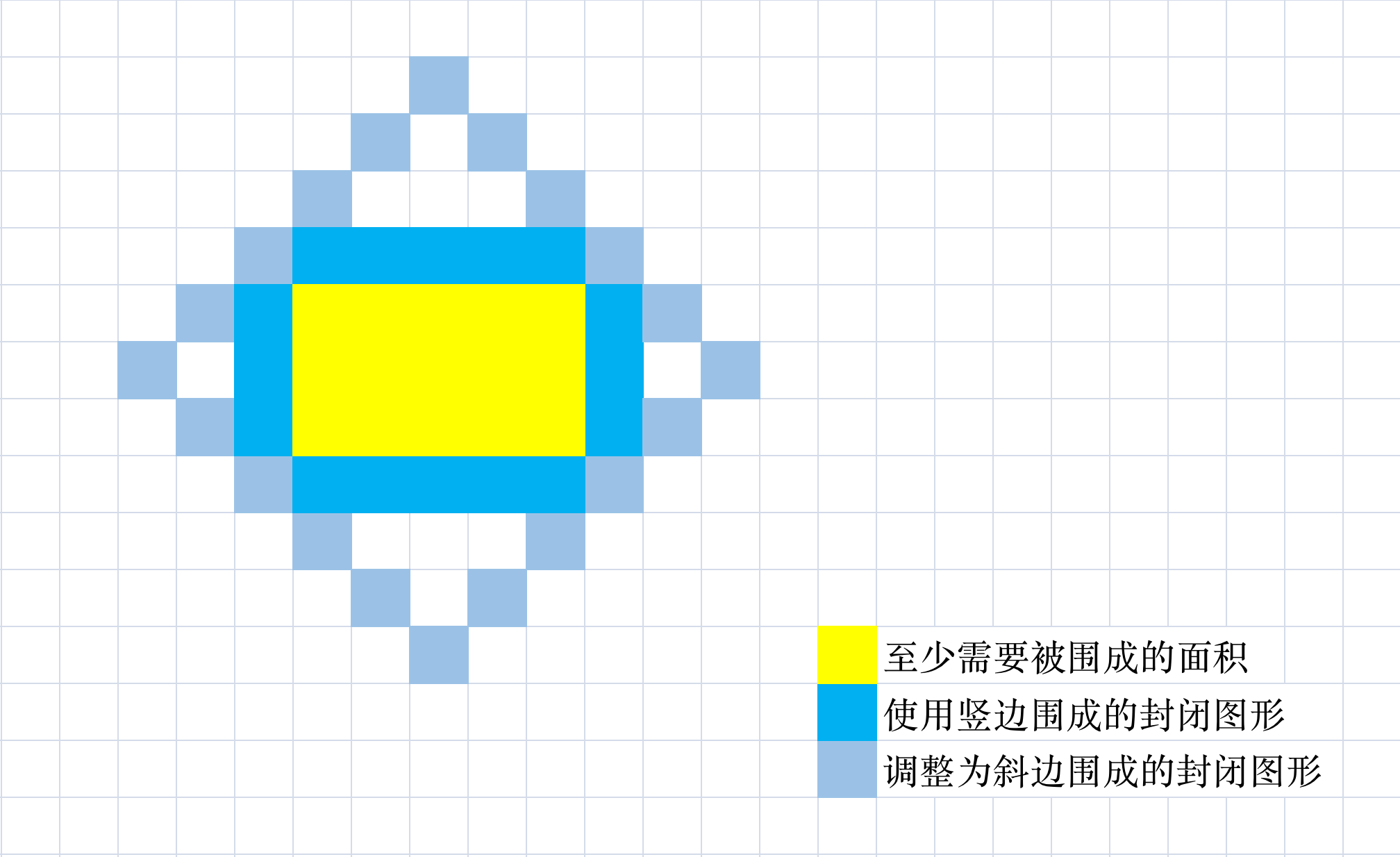
即组成封闭图形的边不可能有直边，同时由于是封闭图形，因此斜边直接必然是单点衔接，而不可能是平行（无法封闭）。

同时，想要达到最大面积，应当尽可能利用边界作为围成图形的某些边。

利用边界所能围成的最大封面图形 可以是「由边界提供两边，障碍物提供一边的三角形」。

如果不是该形状，则可以通过调整障碍物的直边为一条完整的斜边，来组成封闭三角形，围成面积不会变小：

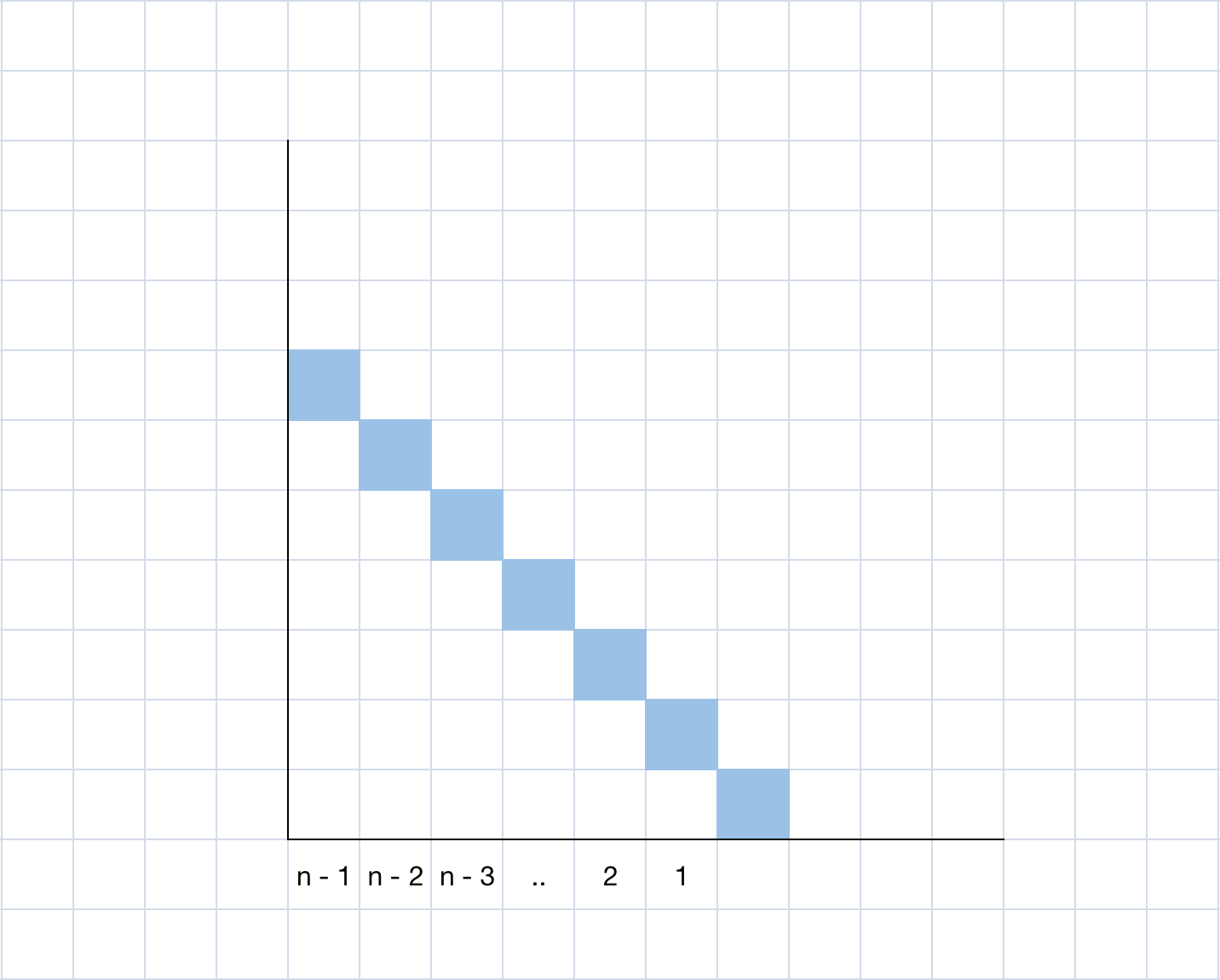
即给定 $n$ 的情况下，根据「等差数列求和」可知，最大所能围成的面积为 $1 + 2 + … + n - 1 = \frac{n \times (n - 1)}{2}$。

因此如果从 $s$ 和 $t$ 出发，能够访问的点数超过 $\frac{n \times (n - 1)}{2}$ 个，那么两点并没有被围住，必然联通。

最后，为了在 BFS 过程中记录某些点被访问过，可以通过计算某个位置哈希值（数值）来实现。

代码（感谢 @🍭可乐可乐吗QAQ 和 @Benhao 同学提供的其他语言版本）：

class Solution {
    int EDGE = (int)1e6, MAX = (int)1e5;
    long BASE = 131L;
    Set<Long> set = new HashSet<>();
    int[][] dir = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
    public boolean isEscapePossible(int[][] blocked, int[] s, int[] t) {
        for (int[] p : blocked) set.add(p[0] * BASE + p[1]);
        int n = blocked.length;
        MAX = n * (n - 1) / 2; // 可直接使用 1e5
        return check(s, t) && check(t, s);
    }
    boolean check(int[] a, int[] b) {
        Set<Long> vis = new HashSet<>();
        Deque<int[]> d = new ArrayDeque<>();
        d.addLast(a);
        vis.add(a[0] * BASE + a[1]);
        while (!d.isEmpty() && vis.size() <= MAX) {
            int[] poll = d.pollFirst();
            int x = poll[0], y = poll[1];
            if (x == b[0] && y == b[1]) return true;
            for (int[] di : dir) {
                int nx = x + di[0], ny = y + di[1];
                if (nx < 0 || nx >= EDGE || ny < 0 || ny >= EDGE) continue;
                long hash = nx * BASE + ny;
                if (set.contains(hash)) continue;
                if (vis.contains(hash)) continue;
                d.addLast(new int[]{nx, ny});
                vis.add(hash);
            }
        }
        return vis.size() > MAX;
    }
}

-

class Solution {
public:
    int EDGE = 1e6, MAX = 1e5;
    long long BASE = 13331;
    unordered_set<long long> set;
    int dir[4][2] = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };
    bool isEscapePossible(vector<vector<int>>& blocked, vector<int>& s, vector<int>& t) {
        for(auto& p : blocked) set.insert(p[0] * BASE + p[1]);
        int n = blocked.size();
        MAX = n * (n - 1) / 2; // 可直接使用 1e5
        return check(s, t) and check(t, s);
    }
    bool check(vector<int>& a, vector<int>& b){
        unordered_set<long long> vis;
        queue< pair<int,int> > q;
        q.push( {a[0], a[1]});
        vis.insert(a[0] * BASE + a[1]);
        while(q.size() and vis.size() <= MAX){
            auto t = q.front();
            q.pop();
            int x = t.first, y = t.second;
            if(x == b[0] and y == b[1]) return true;
            for(int i = 0; i < 4; i++){
                int nx = x + dir[i][0], ny = y + dir[i][1];
                if(nx < 0 or nx >= EDGE or ny < 0 or ny >= EDGE) continue;
                if(set.count(nx * BASE + ny)) continue;
                if(vis.count(nx * BASE + ny)) continue;
                q.push( {nx, ny} );
                vis.insert(nx * BASE + ny);
            }
        }
        return vis.size() > MAX;
    }
};

-

EDGE, MAX, BASE, DIR = int(1e6), int(1e5), 131, [(1, 0), (-1, 0), (0, 1), (0, -1)]
class Solution:
    def isEscapePossible(self, blocked: List[List[int]], source: List[int], target: List[int]) -> bool:
        block = {p[0] * BASE + p[1] for p in blocked}
        n = len(blocked)
        MAX = n * (n-1)//2 # 可直接使用 1e5
        def check(a, b):
            vis = {a[0] * BASE + a[1]}
            d = deque([a])
            while len(d) and len(vis) <= MAX:
                x, y = d.popleft()
                if x == b[0] and y == b[1]:
                    return True
                for dx, dy in DIR:
                    nx, ny = x + dx, y + dy
                    if nx < 0 or nx >= EDGE or ny < 0 or ny >= EDGE:
                        continue
                    h = nx * BASE + ny
                    if h in block or h in vis:
                        continue
                    d.append((nx, ny))
                    vis.add(h)
            return len(vis) > MAX
        return check(source, target) and check(target, source)

• 时间复杂度：令 $n$ 为 $blocked$ 大小，两次 BFS 的最大访问点数为 $\frac{n \times (n - 1)}{2}$。整体复杂度为 $O(n^2)$
• 空间复杂度：两次 BFS 的最大访问点数为 $\frac{n \times (n - 1)}{2}$。整体复杂度为 $O(n^2)$

---

最后

这是我们「刷穿 LeetCode」系列文章的第 No.1036 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。