LC 1610. 可见点的最大数目
题目描述
这是 LeetCode 上的 1610. 可见点的最大数目 ,难度为 困难。
给你一个点数组 points 和一个表示角度的整数 angle ,你的位置是 location,其中 $location = [pos_x, pos_y]$ 且 $points[i] = [x_i, y_i]$ 都表示 X-Y 平面上的整数坐标。
最开始,你面向东方进行观测。你 不能 进行移动改变位置,但可以通过 自转 调整观测角度。换句话说,$pos_x$ 和 $pos_y$ 不能改变。你的视野范围的角度用 angle 表示, 这决定了你观测任意方向时可以多宽。设 d 为你逆时针自转旋转的度数,那么你的视野就是角度范围 $[d - angle/2, d + angle/2]$ 所指示的那片区域。
对于每个点,如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ,那么你就可以看到它。
同一个坐标上可以有多个点。你所在的位置也可能存在一些点,但不管你的怎么旋转,总是可以看到这些点。同时,点不会阻碍你看到其他点。
返回你能看到的点的最大数目。
示例 1: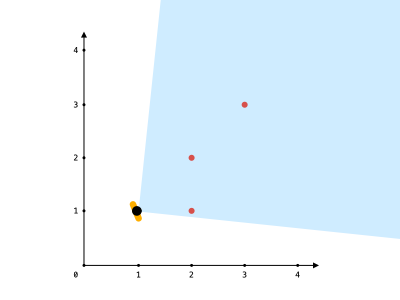
1
2
3
4
5输入:points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
输出:3
解释:阴影区域代表你的视野。在你的视野中,所有的点都清晰可见,尽管 [2,2] 和 [3,3]在同一条直线上,你仍然可以看到 [3,3] 。
示例 2:1
2
3
4
5输入:points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
输出:4
解释:在你的视野中,所有的点都清晰可见,包括你所在位置的那个点。
示例 3: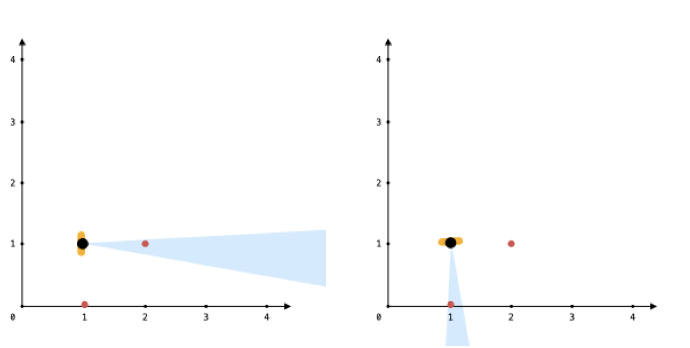
1
2
3
4
5输入:points = [[1,0],[2,1]], angle = 13, location = [1,1]
输出:1
解释:如图所示,你只能看到两点之一。
提示:
- $1 <= points.length <= 10^5$
- $points[i].length == 2$
- $location.length == 2$
- $0 <= angle < 360$
- $0 <= posx, posy, xi, yi <= 100$
数学
这是一道思维难度不大,但细节繁多的题目。
题目要我们旋转出一个角度为 $angle$ 的、可无限延伸的覆盖面,使得该覆盖面所能覆盖 $points$ 中的点最多。
我们所在的位置为 $location = (x,y)$,我们可以将 $(x,y)$ 作为「极点」,求所有 $points[i]$ 的「极角」。
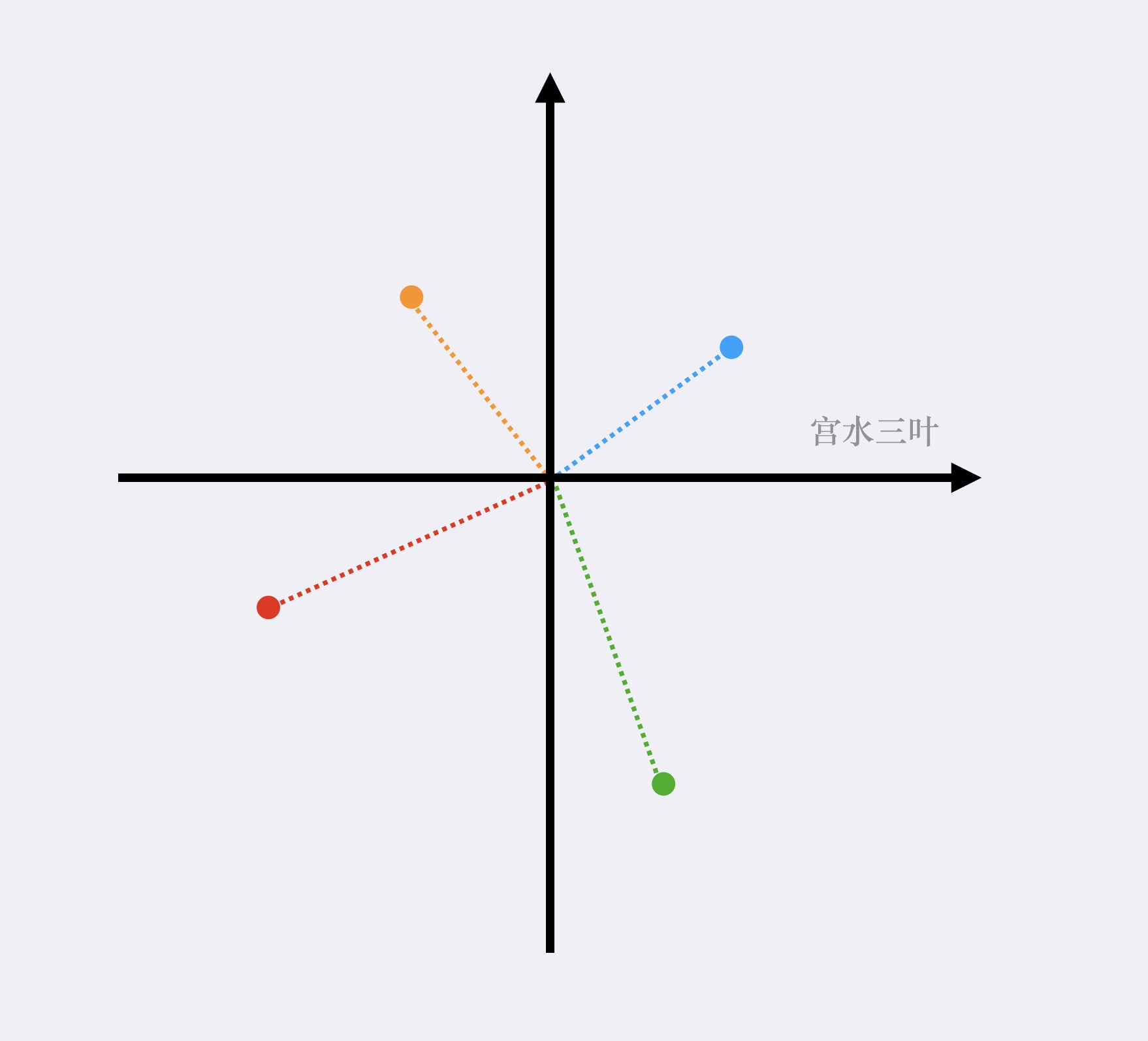
令 $points[i] =(a,b)$,与极点关系 $dx = a - x;dy = b - y$。
求极角的方式有两种:
使用 $atan(\frac{dy}{dx})$:值域范围为 [-90°,90°],需要对 $dx$ 与 $dy$ 进行象限讨论,从而将值域范围转化为我们希望的 [0°,360°],同时需要注意 $dx = 0$ 的边界情况;
使用 $atan2(dy, dx)$:值域范围为 [-180°,180°],与我们期望的 [0°,360°] 相差一个固定的值,可进行统一转换,也可以直接使用。
得到夹角数组 $list$ 后,对其进行排序,问题初步转换为:在夹角数组中找到连续一段 $[i, j]$,使得 $list[i]$ 和 $list[j]$ 的角度差不超过 $angle$。
但直接在原数组 $list$ 操作,会漏掉夹角横跨一四象限的情况:
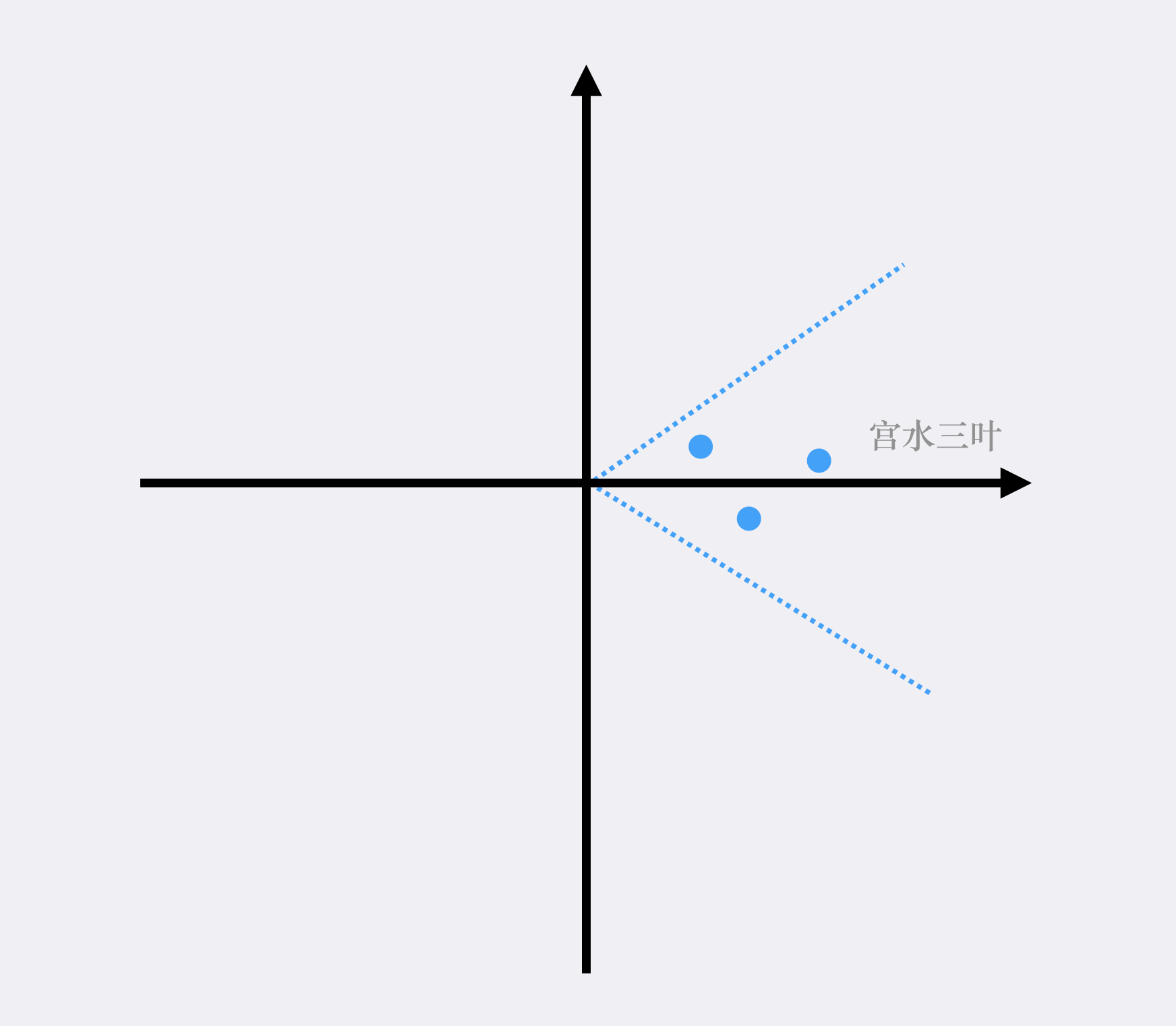
因此,另外一个细节是,在求连续段长度时,先对夹角数组进行拷贝拼接,并对拼接部分增加偏移量(确保数组仍具有单调性)。
具体的,设夹角数组长度为 $n$,此时令 $list[n + i] = list[i] + 2 * PI$,从而将问题彻底转换为求连续段问题。
求解最长合法连续段 $[i,j]$ 可用「双指针」实现「滑动窗口」来做。
一些细节:题目规定了与 $location$ 重合的点在任意角度都能看到,因此我们需要对这些点进行特殊处理,
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public int visiblePoints(List<List<Integer>> points, int angle, List<Integer> location) {
int x = location.get(0), y = location.get(1);
List<Double> list = new ArrayList<>();
int cnt = 0;
double pi = Math.PI, t = angle * pi / 180;
for (List<Integer> p : points) {
int a = p.get(0), b = p.get(1);
if (a == x && b == y && ++cnt >= 0) continue;
list.add(Math.atan2(b - y, a - x) + pi);
}
Collections.sort(list);
int n = list.size(), max = 0;
for (int i = 0; i < n; i++) list.add(list.get(i) + 2 * pi);
for (int i = 0, j = 0; j < 2 * n; j++) {
while (i < j && list.get(j) - list.get(i) > t) i++;
max = Math.max(max, j - i + 1);
}
return cnt + max;
}
}
- 时间复杂度:令 $n$ 为
points数组的长度,预处理出points的所有角度复杂度为 $O(n)$;对所有角度进行排序的复杂度为 $O(n\log{n})$;使用双指针实现滑动窗口得出最大合法子数组的复杂度为 $O(n)$;整体复杂度为 $O(n\log{n})$ - 空间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.1610 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
