LC 319. 灯泡开关
题目描述
这是 LeetCode 上的 319. 灯泡开关 ,难度为 中等。
初始时有 n 个灯泡处于关闭状态。第一轮,你将会打开所有灯泡。接下来的第二轮,你将会每两个灯泡关闭一个。
第三轮,你每三个灯泡就切换一个灯泡的开关(即,打开变关闭,关闭变打开)。
第 i 轮,你每 i 个灯泡就切换一个灯泡的开关。直到第 n 轮,你只需要切换最后一个灯泡的开关。
找出并返回 n 轮后有多少个亮着的灯泡。
示例 1: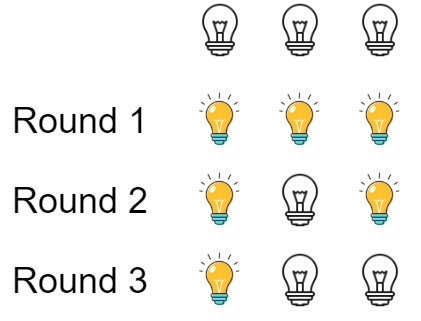
1
2
3
4
5
6
7
8
9
10
11输入:n = 3
输出:1
解释:
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭].
你应该返回 1,因为只有一个灯泡还亮着。
示例 2:1
2
3输入:n = 0
输出:0
示例 3:1
2
3输入:n = 1
输出:1
提示:
- $0 <= n <= 10^9$
数学
这是一道经典的数论题。
整理一下题意:第 $i$ 轮改变所有编号为 $i$ 的倍数的灯泡的状态(其中灯泡编号从 $1$ 开始)。
一个编号为 $x$ 的灯泡经过 $n$ 轮后处于打开状态的充要条件为「该灯泡被切换状态次数为奇数次」。
同时,一个灯泡切换状态的次数为其约数的个数(去重)。
于是问题转换为:在 $[1,n]$ 内有多少个数,其约数的个数为奇数。这些约数个数为奇数的灯泡就是最后亮着的灯泡。
又根据「约数」的定义,我们知道如果某个数 $k$ 为 $x$ 的约数,那么 $\frac{x}{k}$ 亦为 $x$ 的约数,即「约数」总是成对出现,那么某个数的约数个数为奇数,意味着某个约数在分解过程中出现了 $2$ 次,且必然重复出现在同一次拆解中,即 $k = \frac{x}{k}$,即有 $x$ 为完全平方数(反之亦然)。
问题最终转换为:在 $[1,n]$ 中完全平方数的个数为多少。
根据数论推论,$[1,n]$ 中完全平方数的个数为 $\left \lfloor \sqrt{n} \right \rfloor$,即最后亮着的灯泡数量为 $\left \lfloor \sqrt{n} \right \rfloor$。
代码:1
2
3
4
5class Solution {
public int bulbSwitch(int n) {
return (int)Math.sqrt(n);
}
}
- 时间复杂度:$O(1)$
- 空间复杂度:$O(1)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.319 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
