LC 488. 祖玛游戏

题目描述

这是 LeetCode 上的 488. 祖玛游戏 ，难度为 困难。

你正在参与祖玛游戏的一个变种。

在这个祖玛游戏变体中，桌面上有 一排 彩球，每个球的颜色可能是：红色 'R'、黄色 'Y'、蓝色 'B'、绿色 'G' 或白色 'W' 。你的手中也有一些彩球。

你的目标是 清空 桌面上所有的球。每一回合：

• 从你手上的彩球中选出 任意一颗 ，然后将其插入桌面上那一排球中：两球之间或这一排球的任一端。
• 接着，如果有出现 三个或者三个以上 且 颜色相同 的球相连的话，就把它们移除掉。
  • 如果这种移除操作同样导致出现三个或者三个以上且颜色相同的球相连，则可以继续移除这些球，直到不再满足移除条件。
• 如果桌面上所有球都被移除，则认为你赢得本场游戏。
• 重复这个过程，直到你赢了游戏或者手中没有更多的球。

给你一个字符串 board ，表示桌面上最开始的那排球。另给你一个字符串 hand ，表示手里的彩球。请你按上述操作步骤移除掉桌上所有球，计算并返回所需的 最少 球数。如果不能移除桌上所有的球，返回 -1 。

示例 1：

输入：board = "WRRBBW", hand = "RB"

输出：-1

解释：无法移除桌面上的所有球。可以得到的最好局面是：
- 插入一个 'R' ，使桌面变为 WRRRBBW 。WRRRBBW -> WBBW
- 插入一个 'B' ，使桌面变为 WBBBW 。WBBBW -> WW
桌面上还剩着球，没有其他球可以插入。

示例 2：

输入：board = "WWRRBBWW", hand = "WRBRW"

输出：2

解释：要想清空桌面上的球，可以按下述步骤：
- 插入一个 'R' ，使桌面变为 WWRRRBBWW 。WWRRRBBWW -> WWBBWW
- 插入一个 'B' ，使桌面变为 WWBBBWW 。WWBBBWW -> WWWW -> empty
只需从手中出 2 个球就可以清空桌面。

示例 3：

输入：board = "G", hand = "GGGGG"

输出：2

解释：要想清空桌面上的球，可以按下述步骤：
- 插入一个 'G' ，使桌面变为 GG 。
- 插入一个 'G' ，使桌面变为 GGG 。GGG -> empty
只需从手中出 2 个球就可以清空桌面。

示例 4：

输入：board = "RBYYBBRRB", hand = "YRBGB"

输出：3

解释：要想清空桌面上的球，可以按下述步骤：
- 插入一个 'Y' ，使桌面变为 RBYYYBBRRB 。RBYYYBBRRB -> RBBBRRB -> RRRB -> B
- 插入一个 'B' ，使桌面变为 BB 。
- 插入一个 'B' ，使桌面变为 BBB 。BBB -> empty
只需从手中出 3 个球就可以清空桌面。

提示：

• 1 <= board.length <= 16
• 1 <= hand.length <= 5
• board 和 hand 由字符 'R'、'Y'、'B'、'G' 和 'W' 组成
• 桌面上一开始的球中，不会有三个及三个以上颜色相同且连着的球

---

搜索 + 剪枝

数据范围 $1 <= board.length <= 16$ 和 $1 <= hand.length <= 5$。

为了方便，我们使用 $a$ 和 $b$ 来代指 $board$ 和 $hand$。

但在爆搜过程中同时维持两个字符串构造会超时，考虑使用一个 int 来记录 $hand$ 的使用情况。

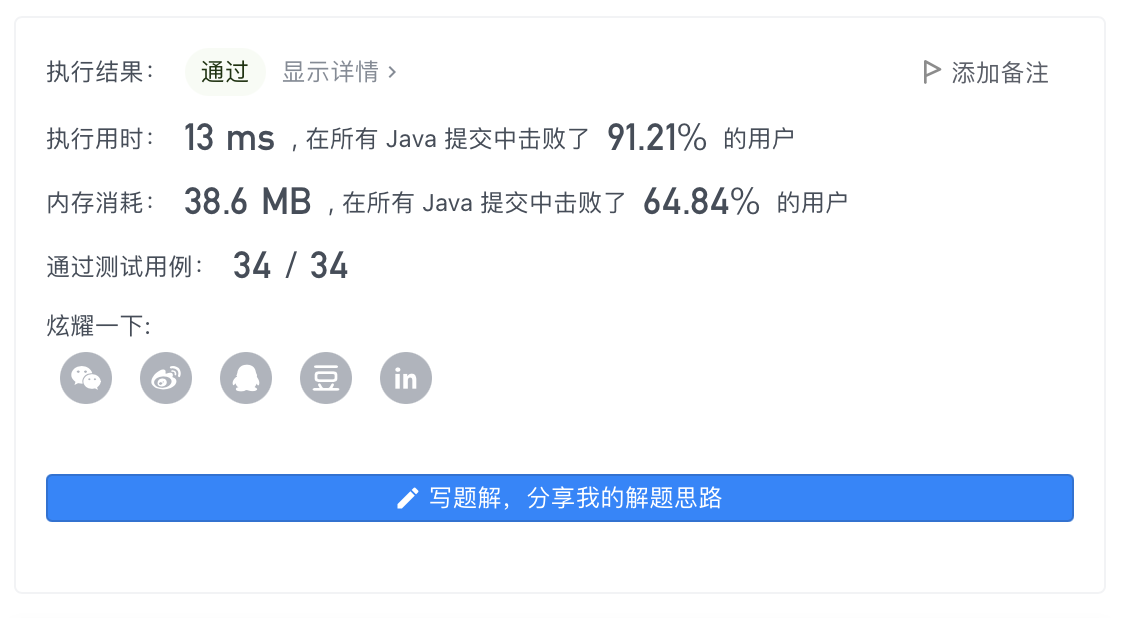
代码：

class Solution {
    int INF = 0x3f3f3f3f;
    String b;
    int m;
    Map<String, Integer> map = new HashMap<>();
    public int findMinStep(String a, String _b) {
        b = _b;
        m = b.length();
        int ans = dfs(a, 1 << m);
        return ans == INF ? -1 : ans;
    }
    int dfs(String a, int cur) {
        if (a.length() == 0) return 0;
        String hashKey = a + "_" + cur;
        if (map.containsKey(hashKey)) return map.get(hashKey);
        int ans = INF;
        int n = a.length();
        for (int i = 0; i < m; i++) {
            if (((cur >> i) & 1) == 1) continue;
            int next = (1 << i) | cur;
            for (int j = 0; j <= n; j++) {
                boolean ok = false;
                if (j > 0 && j < n && a.charAt(j) == a.charAt(j - 1) && a.charAt(j - 1) != b.charAt(i)) ok = true;
                if (j < n && a.charAt(j) == b.charAt(i)) ok = true;
                if (!ok) continue;
                StringBuilder sb = new StringBuilder();
                sb.append(a.substring(0, j)).append(b.substring(i, i + 1));
                if (j != n) sb.append(a.substring(j));
                int k = j;
                while (0 <= k && k < sb.length()) {
                    char c = sb.charAt(k);
                    int l = k, r = k;
                    while (l >= 0 && sb.charAt(l) == c) l--;
                    while (r < sb.length() && sb.charAt(r) == c) r++;
                    if (r - l - 1 >= 3) {
                        sb.delete(l + 1, r);
                        k = l >= 0 ? l : r; 
                    } else {
                        break;
                    }
                }
                ans = Math.min(ans, dfs(sb.toString(), next) + 1);
            }
        }
        map.put(hashKey, ans);
        return ans;
    }
}

• 时间复杂度：略。「爆搜」同时还得考虑「剪枝」的复杂度分析意义不大。
• 空间复杂度：略

---

AStar 算法

我们建立一个类 Node 来代指当前搜索局面。

class Node {
    // 当前的棋盘状况
    String a;
    // cur 代表当前 hand 的使用情况（若 cur 二进制表示中的第 k 位为 1，代表 hand 的第 k 个彩球已被使用）
    // val 代表「当前棋盘为 a」和「hand 使用情况为 cur」的情况下，至少还需要多少步才能将 a 全部消掉（启发式估算值）
    // step 代表当前局面是经过多少步而来
    int cur, val, step;
    Node (String _a, int _c, int _v, int _s) {
        a = _a;
        cur = _c; val = _v; step = _s;
    }
}

显然，直接对此进行 BFS，会 TLE。

我们考虑将优化 BFS 中使用到的队列改为优先队列：更接近答案的局面先出队进行局面延展。

然后我们考虑如何设计 AStar 的启发式函数。

首先，一个合格的 AStar 启发式函数应当能够确保「估值不会小于理论最小距离」。同时由于启发式的估值函数是针对于最终状态进行估算，因此只确保最终状态的第一次出队时为最短路，其余中间状态的首次出队不一定是最短路，为此我们需要使用哈希表来记录中间状态的距离变化，如果某个局面的最短距离被更新，我们应当将其再次入队。

基于此，我们设计如下的 AStar 的启发式函数：使用哈希表来统计「当前的棋盘 $a$ 的彩球数量」&「当前手上拥有的彩球数量」，对「无解情况」和「理论最小次数」进行分析：

• 对于某个彩球 $c$ 而言，如果当前棋盘的数量 + 手上的数量 都不足 $3$ 个，那么该局面往下搜索也必然无解，该局面无须入队；
• 对于某个彩球 $c$ 而言，如果当前棋盘数量少于 $3$ 个，那么至少需要补充至 $3$ 个才能被消除，而缺少的个数则是「从手上彩球放入棋盘内」的次数，即对于彩球 $c$，我们理论上至少需要消耗 $3 - cnt$ 次（$cnt$ 为当前棋盘拥有的彩球 $c$ 的数量）。

需要注意的是：对于某个局面 $node$ 而言，最终的距离是由「已确定距离」+「估值距离」两部分组成，我们应当根据这两部分之和进行出队，才能确保算法的正确性。

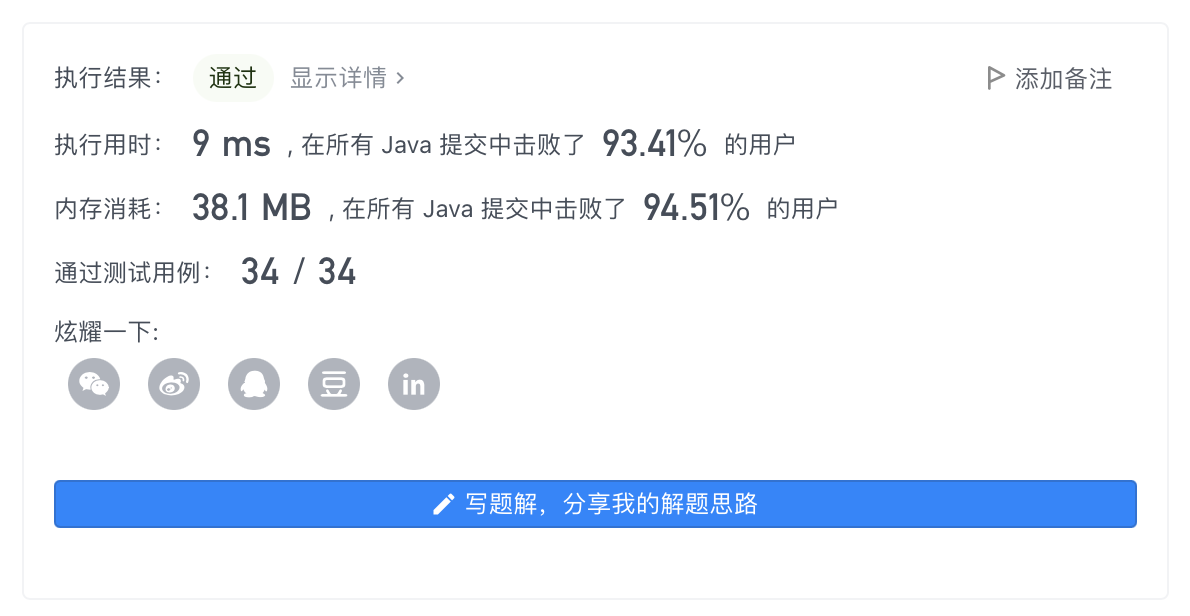
代码：

class Solution {
    class Node {
        String a;
        int cur, val, step;
        Node (String _a, int _c, int _v, int _s) {
            a = _a;
            cur = _c; val = _v; step = _s;
        }
    }
    int f(String a, int k) {
        Map<Character, Integer> m1 = new HashMap<>(), m2 =  new HashMap<>();
        for (int i = 0; i < a.length(); i++) {
            m1.put(a.charAt(i), m1.getOrDefault(a.charAt(i), 0) + 1);
        }
        for (int i = 0; i < m; i++) {
            if (((k >> i) & 1) == 0) m2.put(b.charAt(i), m2.getOrDefault(b.charAt(i), 0) + 1);
        }
        int ans = 0;
        for (char c : m1.keySet()) {
            int c1 = m1.get(c), c2 = m2.getOrDefault(c, 0);
            if (c1 + c2 < 3) return INF;
            if (c1 < 3) ans += (3 - c1);
        }
        return ans;
    }

    int INF = 0x3f3f3f3f;
    String b;
    int m;
    Map<String, Integer> map = new HashMap<>();
    public int findMinStep(String _a, String _b) {
        b = _b;
        m = b.length();
        PriorityQueue<Node> q = new PriorityQueue<>((o1,o2)->(o1.val+o1.step)-(o2.val+o2.step));
        q.add(new Node(_a, 1 << m, f(_a, 1 << m), 0));
        map.put(_a + "_" + (1 << m), 0);
        while (!q.isEmpty()) {
            Node poll = q.poll();
            String a = poll.a;
            int cur = poll.cur;
            int step = poll.step;
            int n = a.length();
            for (int i = 0; i < m; i++) {
                if (((cur >> i) & 1) == 1) continue;
                int next = (1 << i) | cur;
                for (int j = 0; j <= n; j++) {
                    boolean ok = false;
                    if (j > 0 && j < n && a.charAt(j) == a.charAt(j - 1) && a.charAt(j - 1) != b.charAt(i)) ok = true;
                    if (j < n && a.charAt(j) == b.charAt(i)) ok = true;
                    if (!ok) continue;
                    StringBuilder sb = new StringBuilder();
                    sb.append(a.substring(0, j)).append(b.substring(i, i + 1));
                    if (j != n) sb.append(a.substring(j));
                    int k = j;
                    while (0 <= k && k < sb.length()) {
                        char c = sb.charAt(k);
                        int l = k, r = k;
                        while (l >= 0 && sb.charAt(l) == c) l--;
                        while (r < sb.length() && sb.charAt(r) == c) r++;
                        if (r - l - 1 >= 3) {
                            sb.delete(l + 1, r);
                            k = l >= 0 ? l : r; 
                        } else {
                            break;
                        }
                    }
                    String nextStr = sb.toString();
                    if (nextStr.length() == 0) return step + 1;
                    if (f(nextStr, next) == INF) continue;
                    String hashKey = nextStr + "_" + next;
                    if (!map.containsKey(hashKey) || map.get(hashKey) > step + 1) {
                        map.put(hashKey, step + 1);
                        q.add(new Node(nextStr, next, f(nextStr, next), step + 1));
                    }
                }
            }
        }
        return -1;
    }
}

• 时间复杂度：略。「爆搜」同时还得考虑「启发式加速」的复杂度分析意义不大。
• 空间复杂度：略

---

最后

这是我们「刷穿 LeetCode」系列文章的第 No.488 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。