LC 437. 路径总和 III
题目描述
这是 LeetCode 上的 437. 路径总和 III ,难度为 中等。
给定一个二叉树的根节点 root ,和一个整数 targetSum,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1: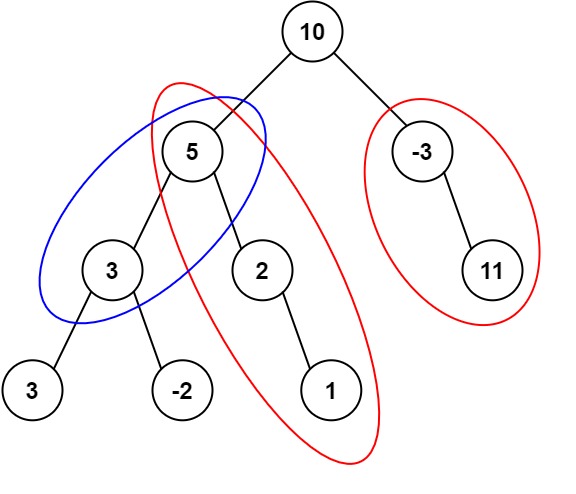
1
2
3
4
5输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
示例 2:1
2
3输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:3
提示:
- 二叉树的节点个数的范围是 [0,1000]
- $-10^9 <= Node.val <= 10^9$
- $-1000 <= targetSum <= 1000$
树的遍历 + DFS
一个朴素的做法是搜索以每个节点为根的(往下的)所有路径,并对路径总和为 $targetSum$ 的路径进行累加统计。
使用 dfs1 来搜索所有节点,复杂度为 $O(n)$;在 dfs1 中对于每个当前节点,使用 dfs2 搜索以其为根的所有(往下的)路径,同时累加路径总和为 $targetSum$ 的所有路径,复杂度为 $O(n)$。
整体复杂度为 $O(n^2)$,数据范围为 $10^3$,可以过。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
int ans, t;
public int pathSum(TreeNode root, int _t) {
t = _t;
dfs1(root);
return ans;
}
void dfs1(TreeNode root) {
if (root == null) return;
dfs2(root, root.val);
dfs1(root.left);
dfs1(root.right);
}
void dfs2(TreeNode root, long val) {
if (val == t) ans++;
if (root.left != null) dfs2(root.left, val + root.left.val);
if (root.right != null) dfs2(root.right, val + root.right.val);
}
}
- 时间复杂度:$O(n^2)$
- 空间复杂度:忽略递归带来的额外空间开销,复杂度为 $O(1)$
树的遍历 + 前缀和
在「解法一」中,我们统计的是以每个节点为根的(往下的)所有路径,也就是说统计的是以每个节点为「路径开头」的所有合法路径。
本题的一个优化切入点为「路径只能往下」,因此如果我们转换一下,统计以每个节点为「路径结尾」的合法数量的话,配合原本就是「从上往下」进行的数的遍历(最完整的路径必然是从原始根节点到当前节点的唯一路径),相当于只需要在完整路径中找到有多少个节点到当前节点的路径总和为 $targetSum$。
于是这个树上问题彻底转换一维问题:求解从原始起点(根节点)到当前节点 $b$ 的路径中,有多少节点 $a$ 满足 $sum[a…b] = targetSum$,由于从原始起点(根节点)到当前节点的路径唯一,因此这其实是一个「一维前缀和」问题。
具体的,我们可以在进行树的遍历时,记录下从原始根节点 $root$ 到当前节点 $cur$ 路径中,从 $root$ 到任意中间节点 $x$ 的路径总和,配合哈希表,快速找到满足以 $cur$ 为「路径结尾」的、使得路径总和为 $targetSum$ 的目标「路径起点」有多少个。
一些细节:由于我们只能统计往下的路径,但是树的遍历会同时搜索两个方向的子树。因此我们应当在搜索完以某个节点为根的左右子树之后,应当回溯地将路径总和从哈希表中删除,防止统计到跨越两个方向的路径。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
Map<Long, Integer> map = new HashMap<>();
int ans, t;
public int pathSum(TreeNode root, int _t) {
if (root == null) return 0;
t = _t;
map.put(0L, 1);
dfs(root, root.val);
return ans;
}
void dfs(TreeNode root, long val) {
if (map.containsKey(val - t)) ans += map.get(val - t);
map.put(val, map.getOrDefault(val, 0) + 1);
if (root.left != null) dfs(root.left, val + root.left.val);
if (root.right != null) dfs(root.right, val + root.right.val);
map.put(val, map.getOrDefault(val, 0) - 1);
}
}
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.437 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
