LC 863. 二叉树中所有距离为 K 的结点
题目描述
这是 LeetCode 上的 863. 二叉树中所有距离为 K 的结点 ,难度为 中等。
给定一个二叉树(具有根结点 root), 一个目标结点 target ,和一个整数值 K 。
返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。
示例 1:1
2
3
4
5
6
7输入:root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出:[7,4,1]
解释:
所求结点为与目标结点(值为 5)距离为 2 的结点,
值分别为 7,4,以及 1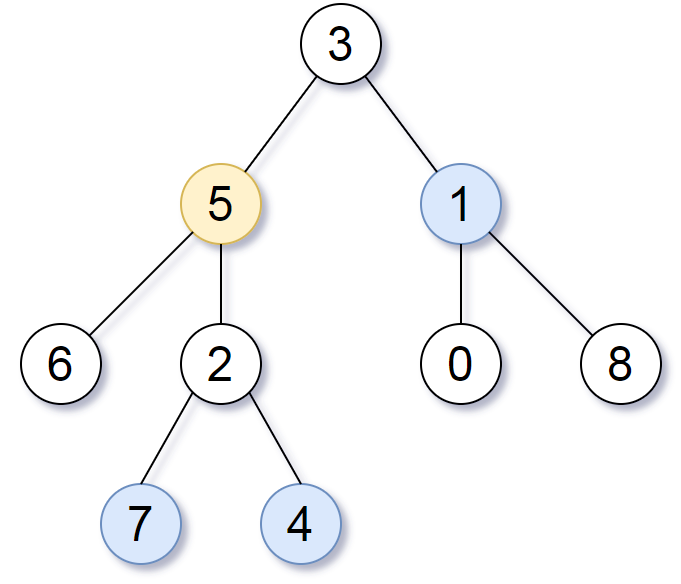
注意,输入的 “root” 和 “target” 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。
提示:
- 给定的树是非空的。
- 树上的每个结点都具有唯一的值 0 <= node.val <= 500 。
- 目标结点 target 是树上的结点。
- 0 <= K <= 1000.
基本分析
显然,如果题目是以图的形式给出的话,我们可以很容易通过「BFS / 迭代加深」找到距离为 $k$ 的节点集。
而树是一类特殊的图,我们可以通过将二叉树转换为图的形式,再进行「BFS / 迭代加深」。
由于二叉树每个点最多有 $2$ 个子节点,点和边的数量接近,属于稀疏图,因此我们可以使用「邻接表」的形式进行存储。
建图方式为:对于二叉树中相互连通的节点(root 与 root.left、root 和 root.right),建立一条无向边。
建图需要遍历整棵树,使用 DFS 或者 BFS 均可。
由于所有边的权重均为 $1$,我们可以使用 「BFS / 迭代加深」 找到从目标节点 target 出发,与目标节点距离为 $k$ 的节点,然后将其添加到答案中。
一些细节:利用每个节点具有唯一的值,我们可以直接使用节点值进行建图和搜索。
建图 + BFS
由「基本分析」,可写出「建图 + BFS」的实现。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51class Solution {
int N = 1010, M = N * 2;
int[] he = new int[N], e = new int[M], ne = new int[M];
int idx;
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
boolean[] vis = new boolean[N];
public List<Integer> distanceK(TreeNode root, TreeNode t, int k) {
List<Integer> ans = new ArrayList<>();
Arrays.fill(he, -1);
dfs(root);
Deque<Integer> d = new ArrayDeque<>();
d.addLast(t.val);
vis[t.val] = true;
while (!d.isEmpty() && k >= 0) {
int size = d.size();
while (size-- > 0) {
int poll = d.pollFirst();
if (k == 0) {
ans.add(poll);
continue;
}
for (int i = he[poll]; i != -1 ; i = ne[i]) {
int j = e[i];
if (!vis[j]) {
d.addLast(j);
vis[j] = true;
}
}
}
k--;
}
return ans;
}
void dfs(TreeNode root) {
if (root == null) return;
if (root.left != null) {
add(root.val, root.left.val);
add(root.left.val, root.val);
dfs(root.left);
}
if (root.right != null) {
add(root.val, root.right.val);
add(root.right.val, root.val);
dfs(root.right);
}
}
}
- 时间复杂度:通过
DFS进行建图的复杂度为 $O(n)$;通过BFS找到距离 $target$ 为 $k$ 的节点,复杂度为 $O(n)$。整体复杂度为 $O(n)$ - 空间复杂度:$O(n)$
建图 + 迭代加深
由「基本分析」,可写出「建图 + 迭代加深」的实现。
迭代加深的形式,我们只需要结合题意,搜索深度为 $k$ 的这一层即可。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45class Solution {
int N = 1010, M = N * 2;
int[] he = new int[N], e = new int[M], ne = new int[M];
int idx;
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
boolean[] vis = new boolean[N];
public List<Integer> distanceK(TreeNode root, TreeNode t, int k) {
List<Integer> ans = new ArrayList<>();
Arrays.fill(he, -1);
dfs(root);
vis[t.val] = true;
find(t.val, k, 0, ans);
return ans;
}
void find(int root, int max, int cur, List<Integer> ans) {
if (cur == max) {
ans.add(root);
return ;
}
for (int i = he[root]; i != -1; i = ne[i]) {
int j = e[i];
if (!vis[j]) {
vis[j] = true;
find(j, max, cur + 1, ans);
}
}
}
void dfs(TreeNode root) {
if (root == null) return;
if (root.left != null) {
add(root.val, root.left.val);
add(root.left.val, root.val);
dfs(root.left);
}
if (root.right != null) {
add(root.val, root.right.val);
add(root.right.val, root.val);
dfs(root.right);
}
}
}
- 时间复杂度:通过
DFS进行建图的复杂度为 $O(n)$;通过迭代加深找到距离 $target$ 为 $k$ 的节点,复杂度为 $O(n)$。整体复杂度为 $O(n)$ - 空间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.863 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
