LC 1846. 减小和重新排列数组后的最大元素

题目描述

这是 LeetCode 上的 1846. 减小和重新排列数组后的最大元素 ，难度为中等。

给你一个正整数数组 arr。

请你对 arr 执行一些操作（也可以不进行任何操作），使得数组满足以下条件：

arr 中第一个元素必须为 1 。
任意相邻两个元素的差的绝对值小于等于 $1$ ，也就是说，对于任意的 $1 <= i < arr.length$ （数组下标从 $0$ 开始），都满足 abs(arr[i] - arr[i - 1]) <= 1。abs(x) 为 x 的绝对值。

你可以执行以下 2 种操作任意次：

减小 arr 中任意元素的值，使其变为一个更小的正整数。
重新排列 arr 中的元素，你可以以任意顺序重新排列。

请你返回执行以上操作后，在满足前文所述的条件下，arr 中可能的最大值。

示例 1：

输入：arr = [2,2,1,2,1]

输出：2

解释：
我们可以重新排列 arr 得到 [1,2,2,2,1] ，该数组满足所有条件。
arr 中最大元素为 2 。

示例 2：

输入：arr = [100,1,1000]

输出：3

解释：
一个可行的方案如下：
1. 重新排列 arr 得到 [1,100,1000] 。
2. 将第二个元素减小为 2 。
3. 将第三个元素减小为 3 。
现在 arr = [1,2,3] ，满足所有条件。
arr 中最大元素为 3 。

示例 3：

输入：arr = [1,2,3,4,5]

输出：5

解释：数组已经满足所有条件，最大元素为 5 。

提示：

$1 <= arr.length <= 10^5$
$1 <= arr[i] <= 10^9$

基本分析 & 证明

根据题意，数组的第一位必须是 $1$，且每个数只能减小或不变，数值位置可以任意调整。

求解经过调整后，符合要求的数组中的最大值是多少。

首先符合条件的数组相邻位差值绝对值不超过 $1$，这限定了数组的必然是如下三种分布之一：

（非严格）单调递减
存在波段
（非严格）单调递增

证明一：取得最优解对应的数组「必然是」或者「可调整为」（非严格）单调递增的形式。

我们使用反证法来证明另外两种分布不能取得最优解：

（非严格）单调递减：题目限定了数的范围为正整数，且第一位为 $1$，这种情况不用讨论了，跳过；
存在波段：我们始终可以将波峰的右侧出现的值，纳入到波峰的左侧，从而消掉这个波峰，最终将整个分布调整为「（非严格）单调递增」的形式，结果不会变差：

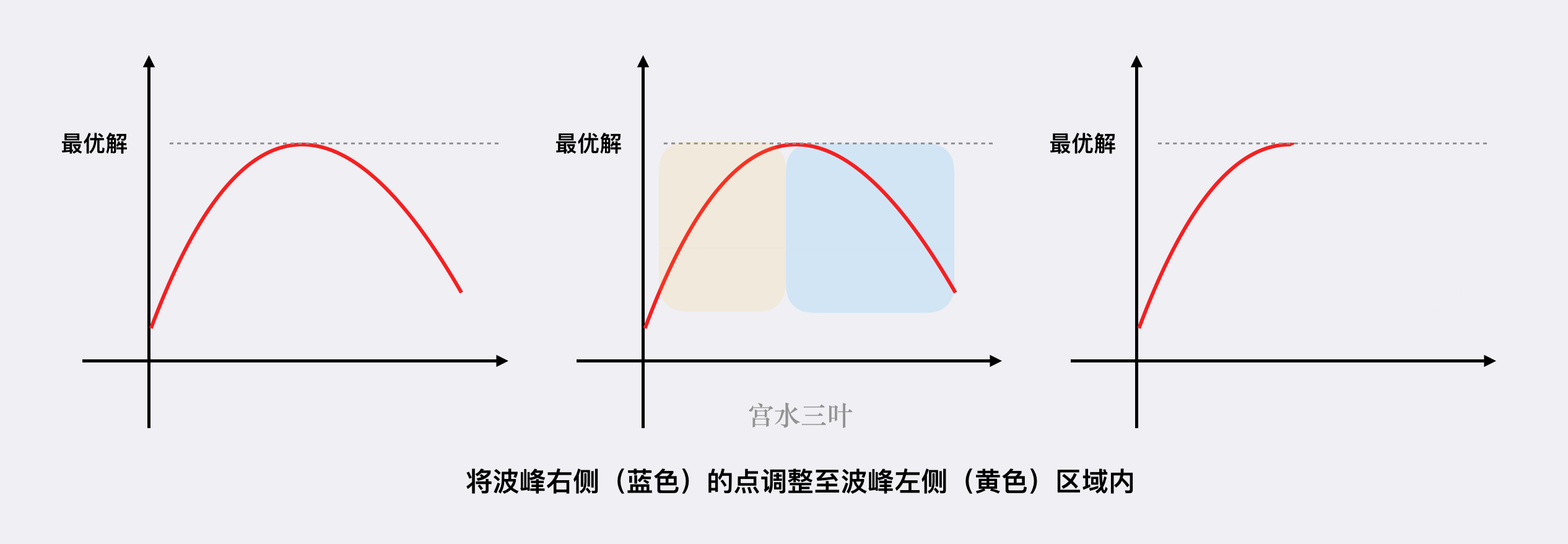
多个波段的情况也是同理，可以自己在纸上画画。

都是利用 波峰右侧的点可以调整成波峰左侧的点，从而使分布变为（非严格）单调递增。

至此，我们证明了最优解对应的数组必然符合（非严格）单调递增。

这启发我们可以先对原数组排个序，在此基础上进行分析。

对原数组排序得到的有序数组，不一定是符合「相邻位差值绝对值不超过 $1$」的，同时由于每个数值可以选择减小或不变。

证明二：当必须要对当前位进行调整的时，优先选择调整为「与前一值差值为 $1$ 的较大数」不会比调整为「与前一差值为 $0$ 的较小数」更差。

这可以使用归纳推理，假设采取「优先调整为与前一值差值为 $1$ 的较大数」得到的序列为 a，采用「优先调整与前一差值为 $0$ 的较小数」得到的序列为 b。

根据「$a[0] = b[0] = 1$」、「a 和 b 长度一致」、「a 和 b 均为（非严格）单调递增」以及「a 和 b 均满足相邻位差值不超过 $1$」，可推导出 $sum(a) >= sum(b)$，和任意位置 $a[i] >= b[i]$，从而推导出 a 序列的最后一位必然大于等于 b 的最后一位。

即 b 不会比 a 更优。

证明三：调整大小的操作不会改变数组元素之间的相对位置关系。

在证明二的分析中，我们会对某些元素进行“减小”操作，使得整个数组最终满足「相邻位差值绝对值不超过 $1$」。

但该证明成立的还有一个很重要的前提条件，就是调整操作不会出发元素的位置重排。

那么该前提条件是否必然成立呢？答案是必然成立。

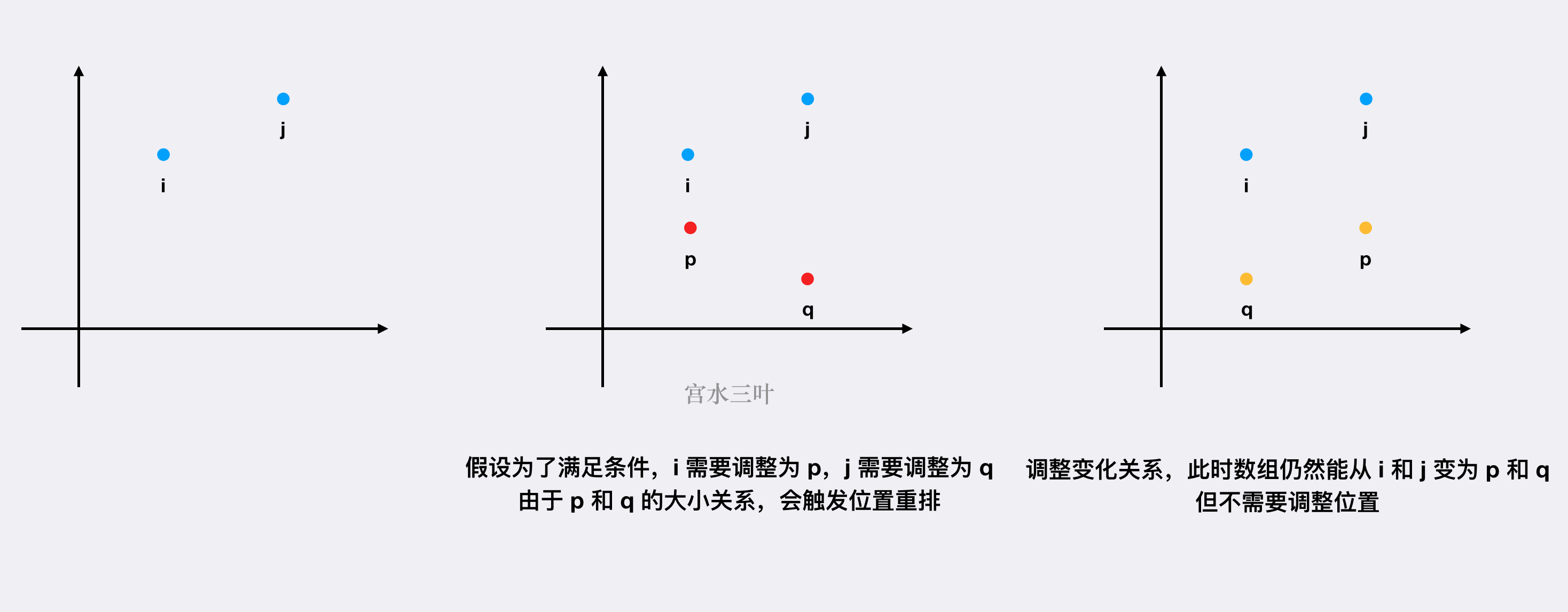
假设原排序数组中存在需要调整的点 $i$ 和点 $j$，且 $nums[i] <= nums[j]$。

为了让数组满足条件，它们都进行了“减少”操作的调整，分别变为了 $p$ 和 $q$，如果触发位置重排的话，必然有 $nums[p] >= nums[q]$。

此时，我们能够通过调整它们的变化关系：点 $i$ 变为点 $q$、点 $j$ 变成点 $p$ 来确保同样满足条件，且不触发元素在有序数组中的位置重排。

贪心

排序，限定第一位值为 $1$，从前往后处理，根据每一位是否「必须修改（与上一位差值是否大于 $1$）」做决策，如果必须被修改，则修改为与前一值差值为 $1$ 的较大数。

Java 代码：

class Solution {
    public int maximumElementAfterDecrementingAndRearranging(int[] arr) {
        int n = arr.length;
        Arrays.sort(arr);
        arr[0] = 1;
        for (int i = 1; i < n; i++) {
            if (arr[i] - arr[i - 1] > 1) {
                arr[i] = arr[i - 1] + 1;
            }
        }
        return arr[n - 1];
    }
}

C++ 代码：

class Solution {
public:
    int maximumElementAfterDecrementingAndRearranging(vector<int>& arr) {
        int n = arr.size();
        sort(arr.begin(), arr.end());
        arr[0] = 1;
        for (int i = 1; i < n; ++i) {
            if (arr[i] - arr[i - 1] > 1) {
                arr[i] = arr[i - 1] + 1;
            }
        }
        return arr.back();
    }
};

Python 代码：

class Solution:
    def maximumElementAfterDecrementingAndRearranging(self, arr: List[int]) -> int:
        n = len(arr)
        arr.sort()
        arr[0] = 1
        for i in range(1, n):
            if arr[i] - arr[i - 1] > 1:
                arr[i] = arr[i - 1] + 1
        return arr[-1]

TypeScript 代码：

function maximumElementAfterDecrementingAndRearranging(arr: number[]): number {
    const n: number = arr.length;
    arr.sort((a, b) => a - b);
    arr[0] = 1;
    for (let i: number = 1; i < n; i++) {
        if (arr[i] - arr[i - 1] > 1) {
            arr[i] = arr[i - 1] + 1;
        }
    }
    return arr[n - 1];  
};

时间复杂度：假定 Arrays.sort 使用的是双轴快排实现。复杂度为 $O(n\log{n})$
空间复杂度：假定 Arrays.sort 使用的是双轴快排实现。复杂度为 $O(\log{n})$

最后

这是我们「刷穿 LeetCode」系列文章的第 No.1846 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。

贪心

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LC 剑指 Offer 53 - I. 在排序数组中查找数字 I 上一篇

LC 1818. 绝对差值和下一篇