LC 127. 单词接龙
题目描述
这是 LeetCode 上的 127. 单词接龙 ,难度为 困难。
字典 wordList 中从单词 beginWord和 endWord 的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是
beginWord。 - 序列中最后一个单词是
endWord。 - 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典
wordList中的单词。
给你两个单词 beginWord和 endWord和一个字典 wordList,找到从 beginWord到 endWord的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 $0$。
示例 1:1
2
3
4
5输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:1
2
3
4
5输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出:0
解释:endWord "cog" 不在字典中,所以无法进行转换。
提示:
- $1 <= beginWord.length <= 10$
- $endWord.length == beginWord.length$
- $1 <= wordList.length <= 5000$
- $wordList[i].length == beginWord.length$
beginWord、endWord和wordList[i]由小写英文字母组成beginWord != endWordwordList中的所有字符串 互不相同
基本分析
根据题意,每次只能替换一个字符,且每次产生的新单词必须在 wordList 出现过。
一个朴素的实现方法是,使用 BFS 的方式求解。
从 beginWord 出发,枚举所有替换一个字符的方案,如果方案存在于 wordList 中,则加入队列中,这样队列中就存在所有替换次数为 $1$ 的单词。然后从队列中取出元素,继续这个过程,直到遇到 endWord 或者队列为空为止。
同时为了「防止重复枚举到某个中间结果」和「记录每个中间结果是经过多少次转换而来」,我们需要建立一个「哈希表」进行记录。
哈希表的 KV 形式为 { 单词 : 由多少次转换得到 }。
当枚举到新单词 str 时,需要先检查是否已经存在与「哈希表」中,如果不存在则更新「哈希表」并将新单词放入队列中。
这样的做法可以确保「枚举到所有由 beginWord 到 endWord 的转换路径」,并且由 beginWord 到 endWord 的「最短转换路径」必然会最先被枚举到。
双向 BFS
经过分析,BFS 确实可以做,但本题的数据范围较大:1 <= beginWord.length <= 10
朴素的 BFS 可能会带来「搜索空间爆炸」的情况。
想象一下,如果我们的 wordList 足够丰富(包含了所有单词),对于一个长度为 $10$ 的 beginWord 替换一次字符可以产生 $10 \times 25$ 个新单词(每个替换点可以替换另外 $25$ 个小写字母),第一层就会产生 $250$ 个单词;第二层会产生超过 $6 \times 10^4$ 个新单词 …
随着层数的加深,这个数字的增速越快,这就是「搜索空间爆炸」问题。
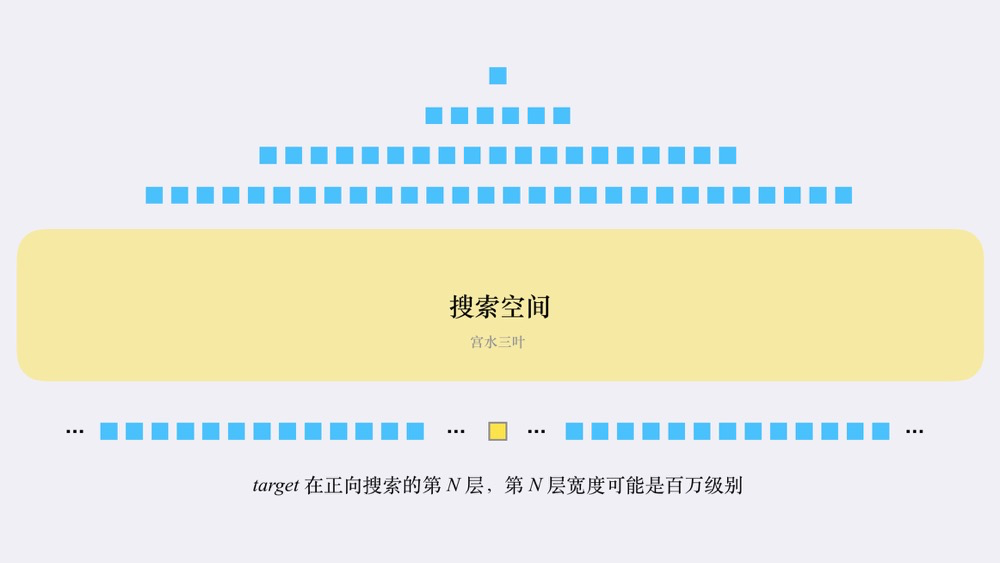
在朴素的 BFS 实现中,空间的瓶颈主要取决于搜索空间中的最大宽度。
那么有没有办法让我们不使用这么宽的搜索空间,同时又能保证搜索到目标结果呢?
「双向 BFS」 可以很好的解决这个问题:
同时从两个方向开始搜索,一旦搜索到相同的值,意味着找到了一条联通起点和终点的最短路径。
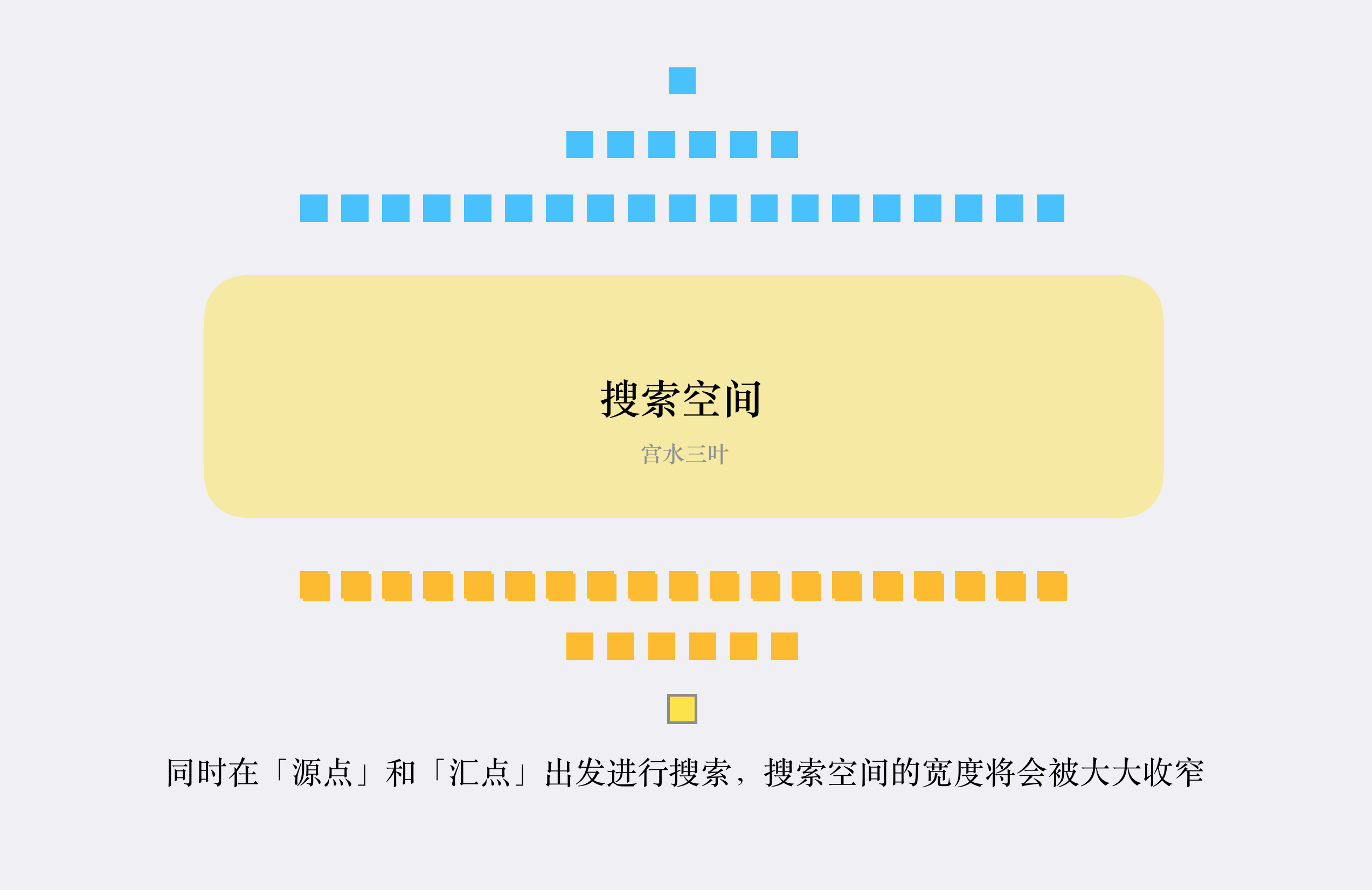
「双向 BFS」的基本实现思路如下:
- 创建「两个队列」分别用于两个方向的搜索;
- 创建「两个哈希表」用于「解决相同节点重复搜索」和「记录转换次数」;
- 为了尽可能让两个搜索方向“平均”,每次从队列中取值进行扩展时,先判断哪个队列容量较少;
- 如果在搜索过程中「搜索到对方搜索过的节点」,说明找到了最短路径。
「双向 BFS」基本思路对应的伪代码大致如下:
1 | |
回到本题,我们看看如何使用「双向 BFS」进行求解。
估计不少同学是第一次接触「双向 BFS」,因此这次我写了大量注释。
建议大家带着对「双向 BFS」的基本理解去阅读。
Java 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82class Solution {
String s, e;
Set<String> set = new HashSet<>();
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
s = beginWord; e = endWord;
// 将所有 word 存入 set,如果目标单词不在 set 中,说明无解
for (String w : wordList) set.add(w);
if (!set.contains(e)) return 0;
int ans = bfs();
return ans == -1 ? 0 : ans + 1;
}
int bfs() {
// d1 代表从起点 beginWord 开始搜索(正向)
// d2 代表从结尾 endWord 开始搜索(反向)
Deque<String> d1 = new ArrayDeque<>(), d2 = new ArrayDeque();
/*
* m1 和 m2 分别记录两个方向出现的单词是经过多少次转换而来
* e.g.
* m1 = {"abc":1} 代表 abc 由 beginWord 替换 1 次字符而来
* m2 = {"xyz":3} 代表 xyz 由 endWord 替换 3 次字符而来
*/
Map<String, Integer> m1 = new HashMap<>(), m2 = new HashMap<>();
d1.add(s);
m1.put(s, 0);
d2.add(e);
m2.put(e, 0);
/*
* 只有两个队列都不空,才有必要继续往下搜索
* 如果其中一个队列空了,说明从某个方向搜到底都搜不到该方向的目标节点
* e.g.
* 例如,如果 d1 为空了,说明从 beginWord 搜索到底都搜索不到 endWord,反向搜索也没必要进行了
*/
while (!d1.isEmpty() && !d2.isEmpty()) {
int t = -1;
// 为了让两个方向的搜索尽可能平均,优先拓展队列内元素少的方向
if (d1.size() <= d2.size()) {
t = update(d1, m1, m2);
} else {
t = update(d2, m2, m1);
}
if (t != -1) return t;
}
return -1;
}
// update 代表从 deque 中取出一个单词进行扩展,
// cur 为当前方向的距离字典;other 为另外一个方向的距离字典
int update(Deque<String> deque, Map<String, Integer> cur, Map<String, Integer> other) {
int m = deque.size();
while (m-- > 0) {
// 获取当前需要扩展的原字符串
String poll = deque.pollFirst();
int n = poll.length();
// 枚举替换原字符串的哪个字符 i
for (int i = 0; i < n; i++) {
// 枚举将 i 替换成哪个小写字母
for (int j = 0; j < 26; j++) {
// 替换后的字符串
String sub = poll.substring(0, i) + String.valueOf((char)('a' + j)) + poll.substring(i + 1);
if (set.contains(sub)) {
// 如果该字符串在「当前方向」被记录过(拓展过),跳过即可
if (cur.containsKey(sub) && cur.get(sub) <= cur.get(poll) + 1) continue;
// 如果该字符串在「另一方向」出现过,说明找到了联通两个方向的最短路
if (other.containsKey(sub)) {
return cur.get(poll) + 1 + other.get(sub);
} else {
// 否则加入 deque 队列
deque.addLast(sub);
cur.put(sub, cur.get(poll) + 1);
}
}
}
}
}
return -1;
}
}
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50class Solution {
public:
string s, e;
unordered_set<string> wordSet;
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
s = beginWord; e = endWord;
for (string w : wordList) wordSet.insert(w);
if (wordSet.find(e) == wordSet.end()) return 0;
int ans = bfs();
return ans == -1 ? 0 : ans + 1;
}
int bfs() {
deque<string> dq1, dq2;
unordered_map<string, int> m1, m2;
dq1.push_back(s);
m1[s] = 0;
dq2.push_back(e);
m2[e] = 0;
while (!dq1.empty() && !dq2.empty()) {
int t = -1;
if (dq1.size() <= dq2.size()) t = update(dq1, m1, m2);
else t = update(dq2, m2, m1);
if (t != -1) return t;
}
return -1;
}
int update(deque<string>& dq, unordered_map<string, int>& cur, unordered_map<string, int>& other) {
int m = dq.size();
while (m-- > 0) {
string poll = dq.front();
dq.pop_front();
int n = poll.length();
for (int i = 0; i < n; i++) {
for (int j = 0; j < 26; j++) {
string sub = poll.substr(0, i) + static_cast<char>('a' + j) + poll.substr(i + 1);
if (wordSet.find(sub) != wordSet.end()) {
if (cur.find(sub) != cur.end() && cur[sub] <= cur[poll] + 1) continue;
if (other.find(sub) != other.end()) {
return cur[poll] + 1 + other[sub];
} else {
dq.push_back(sub);
cur[sub] = cur[poll] + 1;
}
}
}
}
}
return -1;
}
};
Python 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
def bfs():
dq1, dq2 = deque(), deque()
m1, m2 = {}, {}
dq1.append(s)
m1[s] = 0
dq2.append(e)
m2[e] = 0
while dq1 and dq2:
t = update(dq1, m1, m2) if len(dq1) <= len(dq2) else update(dq2, m2, m1)
if t != -1: return t
return -1
def update(dq, cur, other):
m = len(dq)
for _ in range(m):
poll = dq.popleft()
n = len(poll)
for i in range(n):
for j in range(26):
sub = poll[:i] + chr(ord('a') + j) + poll[i+1:]
if sub in wordSet:
if sub in cur and cur[sub] <= cur[poll] + 1: continue
if sub in other:
return cur[poll] + 1 + other[sub]
else:
dq.append(sub)
cur[sub] = cur[poll] + 1
return -1
s, e = beginWord, endWord
wordSet = set(wordList)
if e not in wordSet: return 0
ans = bfs()
return 0 if ans == -1 else ans + 1
- 时间复杂度:令
wordList长度为 $n$,beginWord字符串长度为 $m$。由于所有的搜索结果必须都在wordList出现过,因此算上起点最多有 $n + 1$ 节点,最坏情况下,所有节点都联通,搜索完整张图复杂度为 $O(n^2)$ ;从beginWord出发进行字符替换,替换时进行逐字符检查,复杂度为 $O(m)$。整体复杂度为 $O(m \times n^2)$ - 空间复杂度:同等空间大小。$O(m \times n^2)$
总结
这本质其实是一个「所有边权均为 1」最短路问题:将 beginWord 和所有在 wordList 出现过的字符串看做是一个点。每一次转换操作看作产生边权为 1 的边。问题求以 beginWord 为源点,以 endWord 为汇点的最短路径。
借助这个题,我向你介绍了「双向 BFS」,「双向 BFS」可以有效解决「搜索空间爆炸」问题。
对于那些搜索节点随着层数增加呈倍数或指数增长的搜索问题,可以使用「双向 BFS」进行求解。
启发式搜索 AStar
可以直接根据本题规则来设计 AStar 的「启发式函数」。
比如对于两个字符串 a b 直接使用它们不同字符的数量来充当估值距离,我觉得是合适的。
因为不同字符数量的差值可以确保不会超过真实距离(是一个理论最小替换次数)。
注意:本题数据比较弱,用 AStar 过了,但通常我们需要「确保有解」,AStar 的启发搜索才会发挥真正价值。而本题,除非 endWord 本身就不在 wordList 中,其余情况我们无法很好提前判断「是否有解」。这时候 AStar 将不能带来「搜索空间的优化」,效果不如「双向 BFS」。
Java 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56class Solution {
class Node {
String str;
int val;
Node (String _str, int _val) {
str = _str;
val = _val;
}
}
String s, e;
int INF = 0x3f3f3f3f;
Set<String> set = new HashSet<>();
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
s = beginWord; e = endWord;
for (String w : wordList) set.add(w);
if (!set.contains(e)) return 0;
int ans = astar();
return ans == -1 ? 0 : ans + 1;
}
int astar() {
PriorityQueue<Node> q = new PriorityQueue<>((a,b)->a.val-b.val);
Map<String, Integer> dist = new HashMap<>();
dist.put(s, 0);
q.add(new Node(s, f(s)));
while (!q.isEmpty()) {
Node poll = q.poll();
String str = poll.str;
int distance = dist.get(str);
if (str.equals(e)) {
break;
}
int n = str.length();
for (int i = 0; i < n; i++) {
for (int j = 0; j < 26; j++) {
String sub = str.substring(0, i) + String.valueOf((char)('a' + j)) + str.substring(i + 1);
if (!set.contains(sub)) continue;
if (!dist.containsKey(sub) || dist.get(sub) > distance + 1) {
dist.put(sub, distance + 1);
q.add(new Node(sub, dist.get(sub) + f(sub)));
}
}
}
}
return dist.containsKey(e) ? dist.get(e) : -1;
}
int f(String str) {
if (str.length() != e.length()) return INF;
int n = str.length();
int ans = 0;
for (int i = 0; i < n; i++) {
ans += str.charAt(i) == e.charAt(i) ? 0 : 1;
}
return ans;
}
}
C++ 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53class Solution {
public:
struct Node {
string str;
int val;
Node(string _str, int _val) : str(_str), val(_val) {}
};
string s, e;
const int INF = 0x3f3f3f3f;
unordered_set<string> set;
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
s = beginWord; e = endWord;
for (const string& w : wordList) set.insert(w);
if (set.find(e) == set.end()) return 0;
int ans = astar();
return ans == -1 ? 0 : ans + 1;
}
int astar() {
priority_queue<Node, vector<Node>, function<bool(Node, Node)>> q([](Node a, Node b) {
return a.val > b.val;
});
unordered_map<string, int> dist;
dist[s] = 0;
q.push(Node(s, f(s)));
while (!q.empty()) {
Node poll = q.top();
q.pop();
string str = poll.str;
int distance = dist[str];
if (str == e) break;
int n = str.length();
for (int i = 0; i < n; i++) {
for (int j = 0; j < 26; j++) {
string sub = str.substr(0, i) + char('a' + j) + str.substr(i + 1);
if (set.find(sub) == set.end()) continue;
if (dist.find(sub) == dist.end() || dist[sub] > distance + 1) {
dist[sub] = distance + 1;
q.push(Node(sub, dist[sub] + f(sub)));
}
}
}
}
return dist.find(e) != dist.end() ? dist[e] : -1;
}
int f(string str) {
if (str.length() != e.length()) return INF;
int n = str.length(), ans = 0;
for (int i = 0; i < n; i++) ans += str[i] == e[i] ? 0 : 1;
return ans;
}
};
- 时间复杂度:启发式搜索分析时空复杂度意义不大
- 空间复杂度:启发式搜索分析时空复杂度意义不大
最后
这是我们「刷穿 LeetCode」系列文章的第 No.127 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
