LC 474. 一和零

题目描述

这是 LeetCode 上的 474. 一和零 ，难度为中等。

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的大小，该子集中最多有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的子集。

示例 1：

输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

1
2
3

输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

提示：

1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100

（多维）01 背包

通常与「背包问题」相关的题考察的是 将原问题转换为「背包问题」的能力。

要将原问题转换为「背包问题」，往往需要从题目中抽象出「价值」与「成本」的概念。

这道题如果抽象成「背包问题」的话，应该是：

每个字符串的价值都是 1（对答案的贡献都是 1），选择的成本是该字符串中 1 的数量和 0 的数量。

问我们在 1 的数量不超过 $m$，0 的数量不超过 $n$ 的条件下，最大价值是多少。

由于每个字符串只能被选一次，且每个字符串的选与否对应了「价值」和「成本」，求解的问题也是「最大价值」是多少。

因此可以直接套用 01 背包的「状态定义」来做：

$f[k][i][j]$ 代表考虑前 k 件物品，在数字 1 容量不超过 $i$，数字 0 容量不超过 $j$ 的条件下的「最大价值」（每个字符串的价值均为 1）。

有了「状态定义」之后，「转移方程」也很好推导：

$f[k][i][j] = \max(f[k - 1][i][j], f[k - 1][i - cnt[k][0]][j - cnt[k][1]] + 1)$

其中 $cnt$ 数组记录的是字符串中出现的 $01$ 数量。

代码（为了方便理解，$P1$ 将第一件物品的处理单独抽了出来，也可以不抽出来，只需要将让物品下标从 $1$ 开始即可，见 $P2$）：

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length;
        // 预处理每一个字符包含 0 和 1 的数量
        int[][] cnt = new int[len][2];
        for (int i = 0; i < len; i++) {
            String str = strs[i];
            int zero = 0, one = 0;
            for (char c : str.toCharArray()) {
                if (c == '0') {
                    zero++;
                } else {
                    one++;
                }
            }
            cnt[i] = new int[]{zero, one}; 
        }

        // 处理只考虑第一件物品的情况
        int[][][] f = new int[len][m + 1][n + 1];
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                f[0][i][j] = (i >= cnt[0][0] && j >= cnt[0][1]) ? 1 : 0;
            }
        }

        // 处理考虑其余物品的情况
        for (int k = 1; k < len; k++) {
            int zero = cnt[k][0], one = cnt[k][1];
            for (int i = 0; i <= m; i++) {
                for (int j = 0; j <= n; j++) {
                    // 不选择第 k 件物品
                    int a = f[k-1][i][j];
                    // 选择第 k 件物品（前提是有足够的 m 和 n 额度可使用）
                    int b = (i >= zero && j >= one) ? f[k-1][i-zero][j-one] + 1 : 0;
                    f[k][i][j] = Math.max(a, b);
                }
            }
        }
        return f[len-1][m][n];
    }
}

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length;
        int[][] cnt = new int[len][2];
        for (int i = 0; i < len; i++) {
            String str = strs[i];
            int zero = 0, one = 0;
            for (char c : str.toCharArray()) {
                if (c == '0') zero++;    
                else one++;

            }
            cnt[i] = new int[]{zero, one}; 
        }
        int[][][] f = new int[len + 1][m + 1][n + 1];
        for (int k = 1; k <= len; k++) {
            int zero = cnt[k - 1][0], one = cnt[k - 1][1];
            for (int i = 0; i <= m; i++) {
                for (int j = 0; j <= n; j++) {
                    int a = f[k - 1][i][j];
                    int b = (i >= zero && j >= one) ? f[k - 1][i - zero][j - one] + 1 : 0;
                    f[k][i][j] = Math.max(a, b);
                }
            }
        }
        return f[len][m][n];
    }
}

时间复杂度：预处理字符串的复杂度为 $O(\sum{i = 0}^{k - 1}len(strs[i]))$，处理状态转移的 $O(k m n)$。整体复杂度为：$O(k m n + \sum{i = 0}^{k - 1}len(strs[i]))$
空间复杂度：$O(k m n)$

滚动数组

根据「状态转移」可知，更新某个物品的状态时，只依赖于上一个物品的状态。

因此，可以使用「滚动数组」的方式进行空间优化。

代码（为了方便理解，$P1$ 将第一件物品的处理单独抽了出来，也可以不抽出来，只需要将让物品下标从 $1$ 开始即可，见 $P2$）：

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length;
        // 预处理每一个字符包含 0 和 1 的数量
        int[][] cnt = new int[len][2];
        for (int i = 0; i < len; i++) {
            String str = strs[i];
            int zero = 0, one = 0;
            for (char c : str.toCharArray()) {
                if (c == '0') {
                    zero++;
                } else {
                    one++;
                }
            }
            cnt[i] = new int[]{zero, one}; 
        }

        // 处理只考虑第一件物品的情况
        // 「物品维度」修改为 2 
        int[][][] f = new int[2][m + 1][n + 1];
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                f[0][i][j] = (i >= cnt[0][0] && j >= cnt[0][1]) ? 1 : 0;
            }
        }

        // 处理考虑其余物品的情况
        for (int k = 1; k < len; k++) {
            int zero = cnt[k][0], one = cnt[k][1];
            for (int i = 0; i <= m; i++) {
                for (int j = 0; j <= n; j++) {
                    // 不选择第 k 件物品
                    // 将 k-1 修改为 (k-1)&1
                    int a = f[(k-1)&1][i][j];
                    // 选择第 k 件物品（前提是有足够的 m 和 n 额度可使用）
                    // 将 k-1 修改为 (k-1)&1
                    int b = (i >= zero && j >= one) ? f[(k-1)&1][i-zero][j-one] + 1 : 0;
                    f[k&1][i][j] = Math.max(a, b);
                }
            }
        }
        // 将 len-1 修改为 (len-1)&1
        return f[(len-1)&1][m][n];
    }
}

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length;
        int[][] cnt = new int[len][2];
        for (int i = 0; i < len; i++) {
            String str = strs[i];
            int zero = 0, one = 0;
            for (char c : str.toCharArray()) {
                if (c == '0') zero++;
                else one++; 
            }
            cnt[i] = new int[]{zero, one}; 
        }
        int[][][] f = new int[2][m + 1][n + 1];
        for (int k = 1; k <= len; k++) {
            int zero = cnt[k - 1][0], one = cnt[k - 1][1];
            for (int i = 0; i <= m; i++) {
                for (int j = 0; j <= n; j++) {
                    int a = f[(k-1) & 1][i][j];
                    int b = (i >= zero && j >= one) ? f[(k-1) & 1][i - zero][j - one] + 1 : 0;
                    f[k&1][i][j] = Math.max(a, b);
                }
            }
        }
        return f[len&1][m][n];
    }
}

时间复杂度：预处理字符串的复杂度为 $O(\sum{i = 0}^{k - 1}len(strs[i]))$，处理状态转移的 $O(k m n)$。整体复杂度为：$O(k m n + \sum{i = 0}^{k - 1}len(strs[i]))$
空间复杂度：$O(m * n)$

一维空间优化

事实上，我们还能继续进行空间优化。

再次观察我们的「状态转移方程」发现：$f[k][i][j]$ 不仅仅依赖于上一行，还明确依赖于比 $i$ 小和比 $j$ 小的状态。

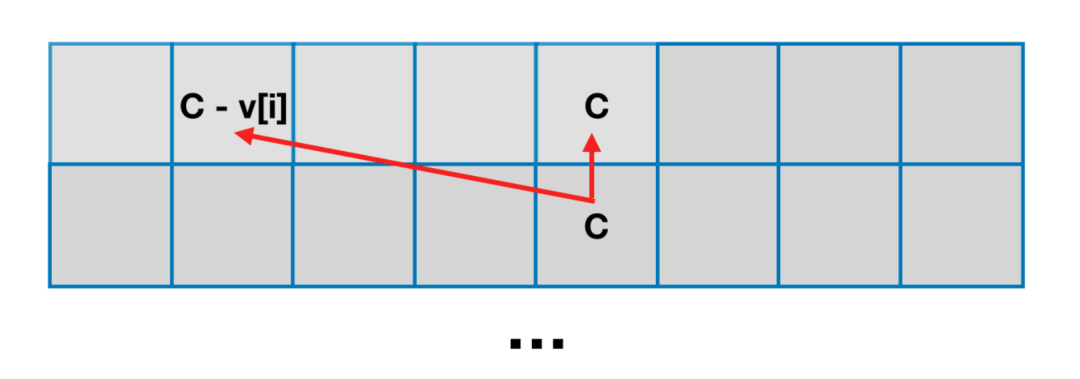
即可只依赖于「上一行」中「正上方」的格子，和「正上方左边」的格子。

对应到「朴素的 01 背包问题」依赖关系如图：

因此可直接参考「01 背包的空间优化」方式：取消掉「物品维度」，然后调整容量的遍历顺序。

代码：

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length;
        int[][] cnt = new int[len][2];
        for (int i = 0; i < len; i++) {
            int zero = 0, one = 0;
            for (char c : strs[i].toCharArray()) {
                if (c == '0') zero++;
                else one++;
            }
            cnt[i] = new int[]{zero, one};
        }
        int[][] f = new int[m + 1][n + 1];
        for (int k = 0; k < len; k++) {
            int zero = cnt[k][0], one = cnt[k][1];
            for (int i = m; i >= zero; i--) {
                for (int j = n; j >= one; j--) {
                    f[i][j] = Math.max(f[i][j], f[i - zero][j - one] + 1);
                }
            }
        }
        return f[m][n];
    }
}

时间复杂度：预处理字符串的复杂度为 $O(\sum{i = 0}^{k - 1}len(strs[i]))$，处理状态转移的 $O(k m n)$。整体复杂度为：$O(k m n + \sum{i = 0}^{k - 1}len(strs[i]))$
空间复杂度：$O(m * n)$

最后

这是我们「刷穿 LeetCode」系列文章的第 No.474 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。

动态规划背包问题 01 背包多维背包

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LC 494. 目标和上一篇

LC 134. 加油站下一篇