LC 134. 加油站

题目描述

这是 LeetCode 上的 134. 加油站 ，难度为中等。

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

说明:

如果题目有解，该答案即为唯一答案。
输入数组均为非空数组，且长度相同。
输入数组中的元素均为非负数。

示例 1:

输入: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出: 3

解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: 
gas  = [2,3,4]
cost = [3,4,3]

输出: -1

解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

基本分析/朴素解法

这是一道比较经典的题目。

估计在 LeetCode 也是有一段时间了，所以连数据范围都没有。

我这里直接规定一下数据范围为 $10^5$，这意味着我们不能使用 $O(n^2)$ 做法了。

但朴素做法往往是优化的出发点，所以我们还是先分析一下，朴素的做法是怎么样的：

题目要求「合法起点」的下标，因此我们可以枚举所有的「起点」
然后按照「油量 & 成本」模拟一遍，看是否能走完一圈

共有 $n$ 个「起点」，检查某个「起点」合法性的复杂度是 $O(n)$ 的。因此整体复杂度为 $O(n^2)$ 的。

代码：

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int n = gas.length;
        for (int start = 0; start < n; start++) {
            // 直接跳过第一步都不满足的起点
            if (gas[start] < cost[start]) continue;
            // 剩余油量
            int cur = gas[start] - cost[start];
            // 所在位置
            int idx = (start + 1) % n;
            while (idx != start) {
                cur += gas[idx] - cost[idx];
                // 如果剩余油量为负数，说明无法离开当前位置，走到下一位置
                if (cur < 0) break;
                idx = (idx + 1) % n;
            }
            if (idx == start) return start;
        }
        return -1;
    }
}

时间复杂度：$O(n^2)$
空间复杂度：$O(1)$

PS. 在 LeetCode 上提交了一下，是可以过的 🤣

KMP

不考虑我们跳过那些第一步就不满足的起点的话，将上述解法中的两个主要逻辑“单独”拎出来看，都是无法优化的：

在没做任何操作之前，我们无法知道哪些起点是不合法的
没有比 $O(n)$ 更低的复杂度可以验证一个起点的合法性

因此只能使用 $O(n^2)$ 解法？

并不是。单独看无法优化，合在一起则可以：随着某个起点「合法性验证」失败，我们可以否决掉一些「必然不合法」的方案。

什么意思呢？

在朴素解法中，当我们验证了某个起点 $i$ 失败（无法走完一圈）之后，我们接下来会去尝试验证起点 $i + 1$。

这时候验证 $i$ 失败过程中产生的“信息”，其实并没有贡献到之后的算法中。

事实上，起点 $i$ 验证失败，其实是意味存在某个位置 $k$ 使得「当前油量」为负数。而这个位置 $k$ 就是验证起点 $i$ 这过程中产生的“信息”。

它可以产生的价值是：在位置 $i$ 和位置 $k$ 之间的所有位置，都不可能是一个合法起点。也就是说，随着起点 $i$ 验证失败，我们可以否决掉方案不仅仅是位置 $i$，而是 $[i, k]$ 这些位置。

我们可以证明为什么会有这样的性质：

首先，可以明确的是：因为 gas 数组和 cost 数组是给定的，因此每个位置的「净消耗」是固定的，与从哪个「起点」出发无关。

净消耗是指该位置提供的「油量」和「到达下一位置的油耗」，也就是 gas[i] 和 cast[i] 之间的差值。

证明过程如图：

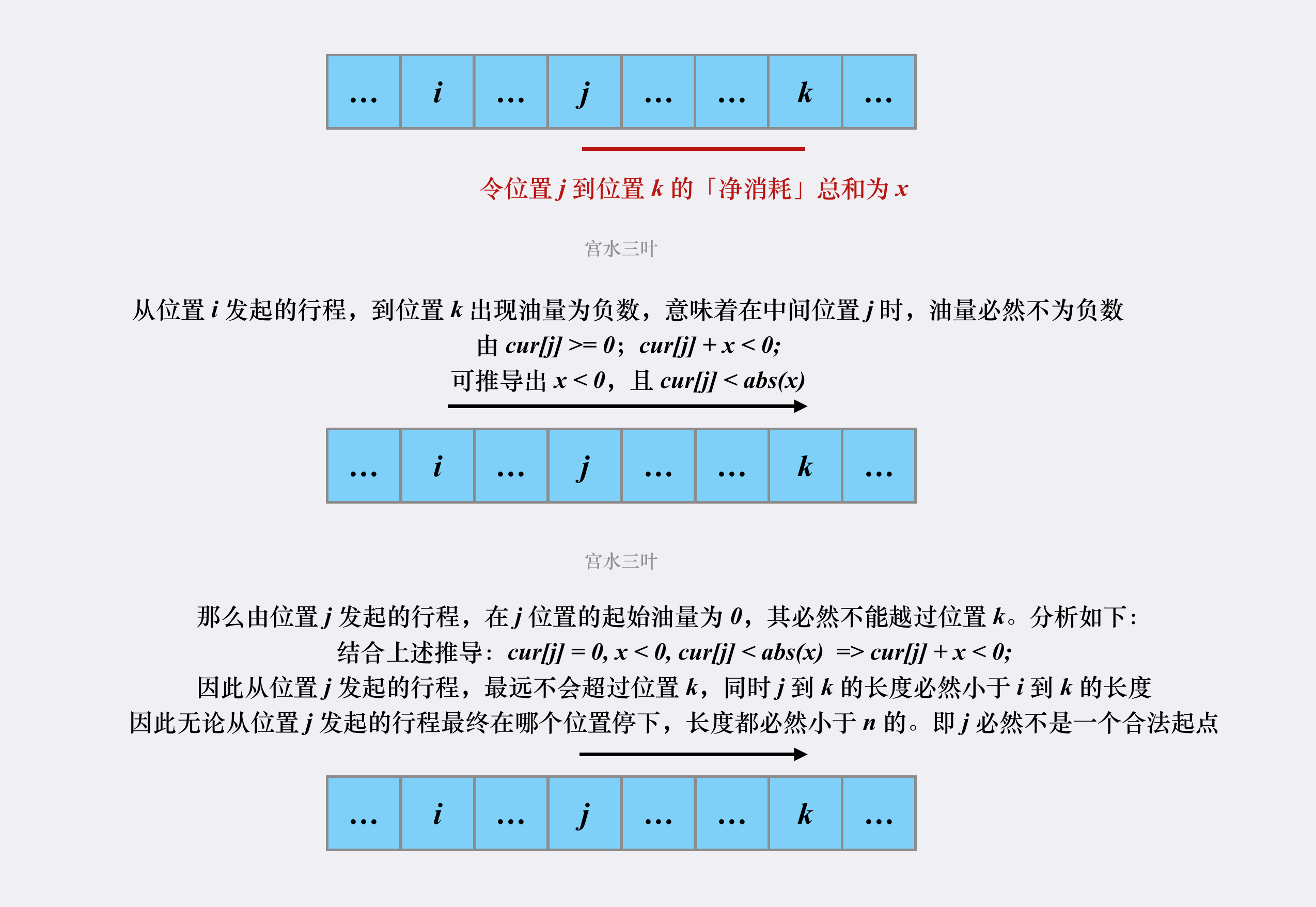
因此，当有了这个优化之后，我们每个位置其实只会被遍历常数次：当位置 $i$ 作为「起点」验证失败后，验证过程中遍历过的位置就不需要再作为「起点」被验证了。

代码：

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int n = gas.length;
        for (int start = 0; start < n; ) {
            if (gas[start] < cost[start]) {
                start++;
            } else {
                int cur = gas[start] - cost[start];
                int idx = start + 1;
                while (idx % n != start) {
                    cur += gas[idx % n] - cost[idx % n];
                    if (cur < 0) break;
                    idx++;
                }
                if (idx % n == start) return start;
                else start = idx;
            }
        }
        return -1;
    }
}

时间复杂度：$O(n)$
空间复杂度：$O(1)$

总结

看到这里，你可以已经理解了 $O(n)$ 解法是怎么来的了。

但可能还不清楚这个优化思路的本质是什么，其实这个优化的本质与 KMP 为什么可以做到线性匹配如出一辙。

本质都是利用某次匹配（验证）过程产生的“信息”，来加速之后的匹配（验证）过程（否决掉一些必然合法的方案）。

在我写过的 KMP 题解里，有这么一句原话：

当我们的原串指针从 i 位置后移到 j 位置，不仅仅代表着「原串」下标范围为 $[i,j)$ 的字符与「匹配串」匹配或者不匹配，更是在否决那些以「原串」下标范围为 $[i,j)$ 为「匹配发起点」的子集。

所以，从更本质的角度出发，这道题其实是一道「KMP」思想应用题，或者说广泛性的「DFA」题。

其他

在写「总结」部分的时候，我还特意去看了一下题解区，没有人提到过「KMP」和「DFA」，几乎所有题解都停留在题目标签「贪心算法」的角度去思考。

这是不对的，题目标签的拟定很大程度取决于「写这个标签的人的水平」和「ta 当时看这道题的思考角度」，是一个主观的结果。

学习算法和数据结构，应该是去理解每个算法和数据结构的“某个操作”为什么能够带来优化效果，并将该优化效果的“底层思想”挖掘出来，应用到我们没见过的问题中，这才是真正的“学习”。

最后

这是我们「刷穿 LeetCode」系列文章的第 No.134 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。

DFA KMP

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LC 474. 一和零上一篇

LC 203. 移除链表元素下一篇