LC 460. LFU 缓存
题目描述
这是 LeetCode 上的 460. LFU 缓存 ,难度为 困难。
请你为最「不经常使用(LFU)」缓存算法设计并实现数据结构。
实现 LFUCache 类:
LFUCache(int capacity)- 用数据结构的容量capacity初始化对象int get(int key)- 如果键存在于缓存中,则获取键的值,否则返回 -1。void put(int key, int value)- 如果键已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量时,则应该在插入新项之前,使最不经常使用的项无效。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除「最近最久未使用」的键。
注意「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。使用次数会在对应项被移除后置为 0 。
为了确定最不常使用的键,可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。
当一个键首次插入到缓存中时,它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作,使用计数器的值将会递增。
示例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26输入:
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出:
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]
解释:
// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序(最左边的元素是最近的)
LFUCache lFUCache = new LFUCache(2);
lFUCache.put(1, 1); // cache=[1,_], cnt(1)=1
lFUCache.put(2, 2); // cache=[2,1], cnt(2)=1, cnt(1)=1
lFUCache.get(1); // 返回 1
// cache=[1,2], cnt(2)=1, cnt(1)=2
lFUCache.put(3, 3); // 去除键 2 ,因为 cnt(2)=1 ,使用计数最小
// cache=[3,1], cnt(3)=1, cnt(1)=2
lFUCache.get(2); // 返回 -1(未找到)
lFUCache.get(3); // 返回 3
// cache=[3,1], cnt(3)=2, cnt(1)=2
lFUCache.put(4, 4); // 去除键 1 ,1 和 3 的 cnt 相同,但 1 最久未使用
// cache=[4,3], cnt(4)=1, cnt(3)=2
lFUCache.get(1); // 返回 -1(未找到)
lFUCache.get(3); // 返回 3
// cache=[3,4], cnt(4)=1, cnt(3)=3
lFUCache.get(4); // 返回 4
// cache=[3,4], cnt(4)=2, cnt(3)=3
提示:
- $0 <= capacity, key, value <= 10^4$
- 最多调用 $10^5$ 次
get和put方法
进阶:你可以为这两种操作设计时间复杂度为 $O(1)$ 的实现吗?
基本分析
前两天我们刚讲过 146. LRU 缓存机制 ,简单理解 LRU 就是「移除最久不被使用的元素」。
因此对于 LRU 我们只需要在使用「哈希表」的同时,维护一个「双向链表」即可:
- 每次发生
get或put的时候就将元素存放双向链表头部 - 当需要移除元素时,则从双向链表尾部开始移除
LFU 简单理解则是指「移除使用次数最少的元素」,如果存在多个使用次数最小的元素,则移除「最近不被使用的那个」(LRU 规则)。同样的 get 和 put 都算作一次使用。
因此,我们需要记录下每个元素的使用次数,并且在 $O(1)$ 的复杂度内「修改某个元素的使用次数」和「找到使用次数最小的元素」。
桶排序 + 双向链表
我们可以使用「桶排序」的思路,搭配「双向链表」实现 $O(1)$ 操作。
在 LFUCache 中,我们维护一个由 Bucket 作为节点的双向链表,每个 Bucket 都有一个 idx 编号,代表当前桶存放的是「使用了多少次」的键值对(idx = 1 的桶存放使用一次的键值对;idx = 2 的桶存放的是使用两次的键值对 … )。
同时 LFUCache 持有一个「哈希表」,用来记录哪些 key 在哪个桶内。
在 Bucket 内部则是维护了一条以 Item 作为节点的双向链表,Item 是用作存放真实键值对的。
同样的,Bucket 也持有一个「哈希表」,用来记录 key 与 Item 的映射关系。
因此 LFUCache 其实是一个「链表套链表」的数据结构:
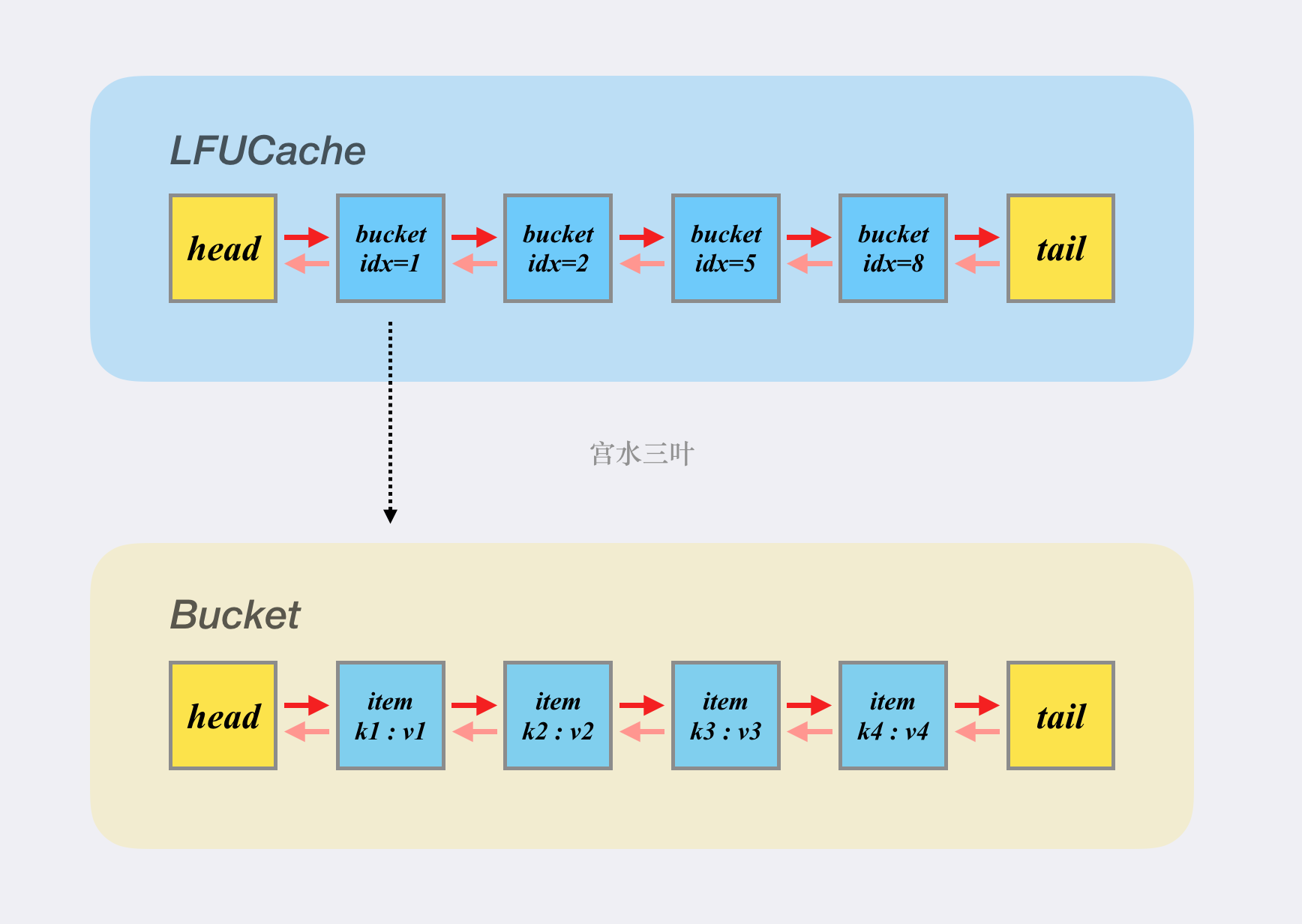
对应到 LFUCache 的几种操作:
get:先通过LFUCache持有的哈希表进行查找,如果不存在返回 $-1$,如果存在找到键值对所在的桶cur:- 调用对应的
cur的remove操作,得到键值对对应的item(移除代表当前键值对使用次数加一了,不会在存在于原来的桶中)。 - 将
item放到idx为 $cur.idx + 1$ 的桶target中(代表代表当前键值对使用次数加一,应该放到新的目标桶中)。 - 如果目标桶
target不存在,则创建;如果原来桶cur移除键值对后为空,则销毁。 - 更新
LFUCache中哈希表的信息。
- 调用对应的
put: 先通过LFUCache持有的哈希表进行查找:- 如果存在:找到键值对所在的桶
cur,调用cur的put操作,更新键值对,然后调用LFUCache的get操作实现使用次数加一。 - 如果不存在:先检查容量是否达到数量:
- 容量达到数量的话需要调用「编号最小的桶」的
clear操作,在clear操作内部,会从item双向链表的尾部开始移除元素。完成后再执行插入操作。
- 容量达到数量的话需要调用「编号最小的桶」的
- 插入操作:将键值对添加到 $idx = 1$ 的桶中(代表当前键值对使用次数为 $1$),如果桶不存在则创建。
- 如果存在:找到键值对所在的桶
Java 代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166class LFUCache {
class Item {
Item l, r;
int k, v;
public Item(int _k, int _v) {
k = _k;
v = _v;
}
}
class Bucket {
Bucket l, r;
int idx;
Item head, tail;
Map<Integer, Item> map = new HashMap<>();
public Bucket(int _idx) {
idx = _idx;
head = new Item(-1, -1);
tail = new Item(-1, -1);
head.r = tail;
tail.l = head;
}
void put(int key, int value) {
Item item = null;
if (map.containsKey(key)) {
item = map.get(key);
// 更新值
item.v = value;
// 在原来的双向链表位置中移除
item.l.r = item.r;
item.r.l = item.l;
} else {
item = new Item(key, value);
// 添加到哈希表中
map.put(key, item);
}
// 增加到双向链表头部
item.r = head.r;
item.l = head;
head.r.l = item;
head.r = item;
}
Item remove(int key) {
if (map.containsKey(key)) {
Item item = map.get(key);
// 从双向链表中移除
item.l.r = item.r;
item.r.l = item.l;
// 从哈希表中移除
map.remove(key);
return item;
}
return null; // never
}
Item clear() {
// 从双向链表尾部找到待删除的节点
Item item = tail.l;
item.l.r = item.r;
item.r.l = item.l;
// 从哈希表中移除
map.remove(item.k);
return item;
}
boolean isEmpty() {
return map.size() == 0;
}
}
Map<Integer, Bucket> map = new HashMap<>();
Bucket head, tail;
int n;
int cnt;
public LFUCache(int capacity) {
n = capacity;
cnt = 0;
head = new Bucket(-1);
tail = new Bucket(-1);
head.r = tail;
tail.l = head;
}
public int get(int key) {
if (map.containsKey(key)) {
Bucket cur = map.get(key);
Bucket target = null;
if (cur.r.idx != cur.idx + 1) {
// 目标桶空缺
target = new Bucket(cur.idx + 1);
target.r = cur.r;
target.l = cur;
cur.r.l = target;
cur.r = target;
} else {
target = cur.r;
}
// 将当前键值对从当前桶移除,并加入新的桶
Item remove = cur.remove(key);
target.put(remove.k, remove.v);
// 更新当前键值对所在桶信息
map.put(key, target);
// 如果在移除掉当前键值对后,当前桶为空,则将当前桶删除(确保空间是 O(n) 的)
// 也确保调用编号最小的桶的 clear 方法,能够有效移除掉一个元素
deleteIfEmpty(cur);
return remove.v;
}
return -1;
}
public void put(int key, int value) {
if (n == 0) return;
if (map.containsKey(key)) {
// 元素已存在,修改一下值
Bucket cur = map.get(key);
cur.put(key, value);
// 调用一下 get 实现「使用次数」+ 1
get(key);
} else {
// 容器已满,需要先删除元素
if (cnt == n) {
// 从第一个桶(编号最小、使用次数最小)中进行清除
Bucket cur = head.r;
Item clear = cur.clear();
map.remove(clear.k);
cnt--;
// 如果在移除掉键值对后,当前桶为空,则将当前桶删除(确保空间是 O(n) 的)
// 也确保调用编号最小的桶的 clear 方法,能够有效移除掉一个元素
deleteIfEmpty(cur);
}
// 需要将当前键值对增加到 1 号桶
Bucket first = null;
// 如果 1 号桶不存在则创建
if (head.r.idx != 1) {
first = new Bucket(1);
first.r = head.r;
first.l = head;
head.r.l = first;
head.r = first;
} else {
first = head.r;
}
// 将键值对添加到 1 号桶
first.put(key, value);
// 更新键值对所在桶信息
map.put(key, first);
// 计数器加一
cnt++;
}
}
void deleteIfEmpty(Bucket cur) {
if (cur.isEmpty()) {
cur.l.r = cur.r;
cur.r.l = cur.l;
cur = null; // help GC
}
}
}
- 时间复杂度:各操作均为 $O(1)$
- 时间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.460 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
