LC 87. 扰乱字符串

题目描述

这是 LeetCode 上的 87. 扰乱字符串 ，难度为困难。

使用下面描述的算法可以扰乱字符串 s 得到字符串 t ：

如果字符串的长度为 1 ，算法停止
如果字符串的长度 > 1 ，执行下述步骤：
- 在一个随机下标处将字符串分割成两个非空的子字符串。即，如果已知字符串 s ，则可以将其分成两个子字符串 x 和 y ，且满足 s = x + y 。
- 随机决定是要「交换两个子字符串」还是要「保持这两个子字符串的顺序不变」。即，在执行这一步骤之后，s 可能是 s = x + y 或者 s = y + x 。
- 在 x 和 y 这两个子字符串上继续从步骤 1 开始递归执行此算法。
  给你两个长度相等的字符串 s1 和 s2，判断 s2 是否是 s1 的扰乱字符串。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：s1 = "great", s2 = "rgeat"

输出：true

解释：s1 上可能发生的一种情形是：
"great" --> "gr/eat" // 在一个随机下标处分割得到两个子字符串
"gr/eat" --> "gr/eat" // 随机决定：「保持这两个子字符串的顺序不变」
"gr/eat" --> "g/r / e/at" // 在子字符串上递归执行此算法。两个子字符串分别在随机下标处进行一轮分割
"g/r / e/at" --> "r/g / e/at" // 随机决定：第一组「交换两个子字符串」，第二组「保持这两个子字符串的顺序不变」
"r/g / e/at" --> "r/g / e/ a/t" // 继续递归执行此算法，将 "at" 分割得到 "a/t"
"r/g / e/ a/t" --> "r/g / e/ a/t" // 随机决定：「保持这两个子字符串的顺序不变」
算法终止，结果字符串和 s2 相同，都是 "rgeat"
这是一种能够扰乱 s1 得到 s2 的情形，可以认为 s2 是 s1 的扰乱字符串，返回 true

示例 2：

1
2
3

输入：s1 = "abcde", s2 = "caebd"

输出：false

示例 3：

1
2
3

输入：s1 = "a", s2 = "a"

输出：true

提示：

s1.length == s2.length
1 <= s1.length <= 30
s1 和 s2 由小写英文字母组成

朴素解法（TLE）

一个朴素的做法根据「扰乱字符串」的生成规则进行判断。

由于题目说了整个生成「扰乱字符串」的过程是通过「递归」来进行。

我们要实现 $isScramble$ 函数的作用是判断 $s1$ 是否可以生成出 $s2$。

这样判断的过程，同样我们可以使用「递归」来做：

假设 $s1$ 的长度为 $n$，的第一次分割的分割点为 $i$，那么 $s1$ 会被分成 $[0, i)$ 和 $[i, n)$ 两部分。

同时由于生成「扰乱字符串」时，可以选交换也可以选不交换。因此我们的 $s2$ 会有两种可能性：

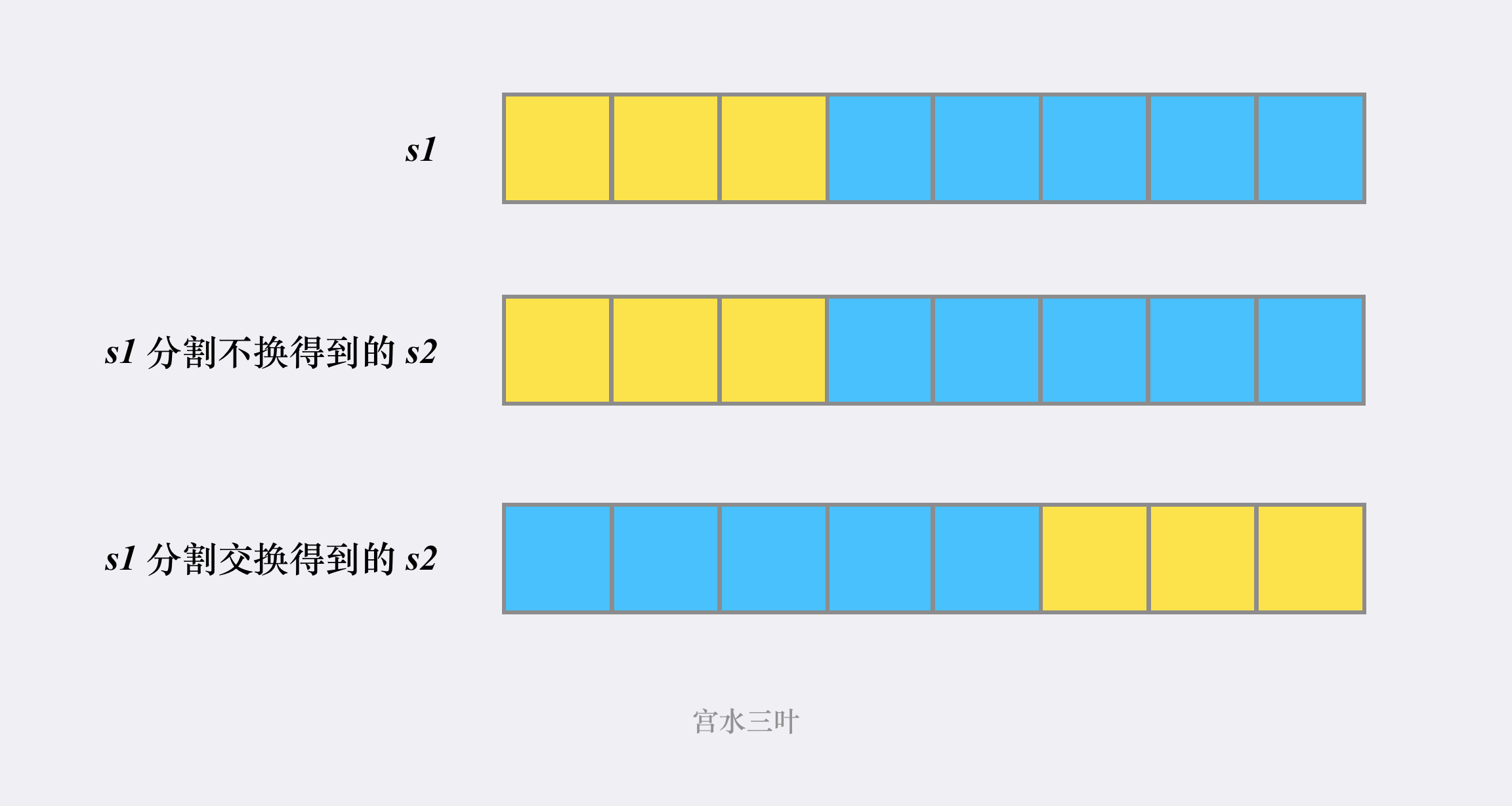
因为对于某个确定的分割点，$s1$ 固定分为两部分，分别为 $[0,i)$ & $[i, n)$。

而 $s2$ 可能会有两种分割方式，分别 $[0,i)$ & $[i,n)$ 和 $[0, n-i)$ & $[n-i,n)$。

我们只需要递归调用 $isScramble$ 检查 $s1$ 的 $[0,i)$ & $[i, n)$ 部分能否与「$s2$ 的 $[0,i)$ & $[i,n)$」或者「$s2$ 的 $[0, n-i)$ & $[n-i,n)$」匹配即可。

同时，我们将「$s1$ 和 $s2$ 相等」和「$s1$ 和 $s2$ 词频不同」作为「递归」出口。

理解这套做法十分重要，后续的解法都是基于此解法演变过来。

代码：

[]

class Solution {
    public boolean isScramble(String s1, String s2) {
        if (s1.equals(s2)) return true;
        if (!check(s1, s2)) return false;
        int n = s1.length();
        for (int i = 1; i < n; i++) {
            // s1 的 [0,i) 和 [i,n)
            String a = s1.substring(0, i), b = s1.substring(i);
            // s2 的 [0,i) 和 [i,n)
            String c = s2.substring(0, i), d = s2.substring(i);
            if (isScramble(a, c) && isScramble(b, d)) return true;
            // s2 的 [0,n-i) 和 [n-i,n)
            String e = s2.substring(0, n - i), f = s2.substring(n - i);
            if (isScramble(a, f) && isScramble(b, e)) return true;
        }
        return false;
    }
    // 检查 s1 和 s2 词频是否相同
    boolean check(String s1, String s2) {
        if (s1.length() != s2.length()) return false;
        int n = s1.length();
        int[] cnt1 = new int[26], cnt2 = new int[26];
        char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
        for (int i = 0; i < n; i++) {
            cnt1[cs1[i] - 'a']++;
            cnt2[cs2[i] - 'a']++;
        }
        for (int i = 0; i < 26; i++) {
            if (cnt1[i] != cnt2[i]) return false;
        }
        return true;
    }
}

时间复杂度：$O(5^n)$
空间复杂度：忽略递归与生成子串带来的空间开销，复杂度为 $O(1)$

记忆化搜索

朴素解法卡在了 $286 / 288$ 个样例。

我们考虑在朴素解法的基础上，增加「记忆化搜索」功能。

我们可以重新设计我们的「爆搜」逻辑：假设 $s1$ 从 $i$ 位置开始，$s2$ 从 $j$ 位置开始，后面的长度为 $len$ 的字符串是否能形成「扰乱字符串」（互为翻转）。

那么在单次处理中，我们可分割的点的范围为 $[1, len)$，然后和「递归」一下，将 $s1$ 分割出来的部分尝试去和 $s2$ 的对应位置匹配。

同样的，我们将「入参对应的子串相等」和「入参对应的子串词频不同」作为「递归」出口。

代码：

[]

class Solution {
    String s1; String s2;
    int n;
    int[][][] cache;
    int N = -1, Y = 1, EMPTY = 0;
    public boolean isScramble(String _s1, String _s2) {
        s1 = _s1; s2 = _s2;
        if (s1.equals(s2)) return true;
        if (s1.length() != s2.length()) return false;
        n = s1.length();
        // cache 的默认值是 EMPTY
        cache = new int[n][n][n + 1];
        return dfs(0, 0, n);
    }
    boolean dfs(int i, int j, int len) {
        if (cache[i][j][len] != EMPTY) return cache[i][j][len] == Y;
        String a = s1.substring(i, i + len), b = s2.substring(j, j + len);
        if (a.equals(b)) {
            cache[i][j][len] = Y;
            return true;
        } 
        if (!check(a, b)) {
            cache[i][j][len] = N;
            return false;
        } 
        for (int k = 1; k < len; k++) {
            // 对应了「s1 的 [0,i) & [i,n)」匹配「s2 的 [0,i) & [i,n)」
            if (dfs(i, j, k) && dfs(i + k, j + k, len - k)) {
                cache[i][j][len] = Y;
                return true;
            }
            // 对应了「s1 的 [0,i) & [i,n)」匹配「s2 的 [n-i,n) & [0,n-i)」
            if (dfs(i, j + len - k, k) && dfs(i + k, j, len - k)) {
                cache[i][j][len] = Y;
                return true;
            }
        }
        cache[i][j][len] = N;
        return false;
    }
    // 检查 s1 和 s2 词频是否相同
    boolean check(String s1, String s2) {
        if (s1.length() != s2.length()) return false;
        int n = s1.length();
        int[] cnt1 = new int[26], cnt2 = new int[26];
        char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
        for (int i = 0; i < n; i++) {
            cnt1[cs1[i] - 'a']++;
            cnt2[cs2[i] - 'a']++;
        }
        for (int i = 0; i < 26; i++) {
            if (cnt1[i] != cnt2[i]) return false;
        }
        return true;
    }
}

时间复杂度：$O(n^4)$
空间复杂度：$O(n^3)$

动态规划（区间 DP）

其实有了上述「记忆化搜索」方案之后，我们就已经可以直接忽略原问题，将其改成「动态规划」了。

根据「dfs 方法的几个可变入参」作为「状态定义的几个维度」，根据「dfs 方法的返回值」作为「具体的状态值」。

我们可以得到状态定义 $f[i][j][len]$：

$f[i][j][len]$ 代表 $s1$ 从 $i$ 开始，$s2$ 从 $j$ 开始，后面长度为 $len$ 的字符是否能形成「扰乱字符串」（互为翻转）。

状态转移方程其实就是翻译我们「记忆化搜索」中的 dfs 主要逻辑部分：

// 对应了「s1 的 [0,i) & [i,n)」匹配「s2 的 [0,i) & [i,n)」
if (dfs(i, j, k) && dfs(i + k, j + k, len - k)) {
    cache[i][j][len] = Y;
    return true;
}
// 对应了「s1 的 [0,i) & [i,n)」匹配「s2 的 [n-i,n) & [0,n-i)」
if (dfs(i, j + len - k, k) && dfs(i + k, j, len - k)) {
    cache[i][j][len] = Y;
    return true;
}

从状态定义上，我们就不难发现这是一个「区间 DP」问题，区间长度大的状态值可以由区间长度小的状态值递推而来。

而且由于本身我们在「记忆化搜索」里面就是从小到大枚举 $len$，因此这里也需要先将 $len$ 这层循环提前，确保我们转移 $f[i][j][len]$ 时所需要的状态都已经被计算好。

代码：

[]

class Solution {
    public boolean isScramble(String s1, String s2) {
        if (s1.equals(s2)) return true;
        if (s1.length() != s2.length()) return false;
        int n = s1.length();
        char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
        boolean[][][] f = new boolean[n][n][n + 1];

        // 先处理长度为 1 的情况
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                f[i][j][1] = cs1[i] == cs2[j];
            }
        }

        // 再处理其余长度情况
        for (int len = 2; len <= n; len++) {
            for (int i = 0; i <= n - len; i++) {
                for (int j = 0; j <= n - len; j++) {
                    for (int k = 1; k < len; k++) {
                        boolean a = f[i][j][k] && f[i + k][j + k][len - k];
                        boolean b = f[i][j + len - k][k] && f[i + k][j][len - k];
                        if (a || b) {
                            f[i][j][len] = true;
                        }
                    }
                }
            }
        }
        return f[0][0][n];
    }
}

时间复杂度：$O(n^4)$
空间复杂度：$O(n^3)$

最后

这是我们「刷穿 LeetCode」系列文章的第 No.87 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。

DFS 记忆化搜索区间 DP

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LC 279. 完全平方数上一篇

LC 213. 打家劫舍 II 下一篇